Глава 3. Стратегии формирования выборки

3.1. Введение

1. В то время как в главе 2 по теме планирования обследований дан общий обзор различных этапов процесса обследования домашних хозяйств, данная глава — это первая из нескольких глав, в которых главный акцент сделан исключительно на тех или иных аспектах выборки, т.е. на основном предмете настоящего руководства. В этой главе дается краткое сравнение вероятностной и детерминированной выборки, а также приводятся аргументы в пользу того, почему последняя должна всегда использоваться в обследованиях домашних хозяйств. Большое внимание уделяется размеру выборки: многим определяющим ее параметрам и способам их расчета. Представлены методы достижения эффективности выборки в обследованиях домашних хозяйств. К ним относятся стратификация, гнездовая выборка и поэтапная выборка с особым упором на двухэтапные планы выборки (см. определения и описания этих понятий в таблице 3.1 и приложении I). Предоставлены различные варианты формирования выборки, а также дается подробное описание двух основных планов выборки, которые были использованы во многих странах. Кроме того, рассмотрены такие специальные темы, как a) формирование выборки в два этапа для охвата «редких» групп населения и b) создание выборки для выявления изменений или трендов. Глава завершается сводным изложением рекомендаций.

3.1.1. Обзор

2. Практически все планы выборки для обследований домашних хозяйств, проводимых как в развитых, так и в развивающихся странах, являются комплексными в силу таких характеристик, как многоэтапность, стратификация и гнездовая выборка. Кроме того, их сложность возрастает в связи с тем фактом, что обследования домашних хозяйств на национальном уровне часто имеют общий характер, охватывая многочисленные темы, интересующие правительство. Поэтому в настоящем руководстве основное внимание уделяется многоэтапным стратегиям выборки.

3. Для получения желаемого результата разработанный надлежащим образом план выборки для обследования домашних хозяйств должен, как симфония, гармонично объединять многочисленные элементы. Формирование выборки должно осуществляться поэтапно с тем, чтобы эффективно выявить места проведения опросов и выбрать домашние хозяйства. План выборки должен быть стратифицирован таким образом, чтобы гарантировать, что фактически сформированная выборка равномерно распределяется по небольшим географическим районам и подгруппам населения. В плане выборки должны использоваться кластеры, обычно представляющие собой географически определенные единицы, из которых отбираются домашние хозяйства, в целях сохранения затрат на управляемом уровне. В то же время следует избегать излишней разбивки на кластеры, поскольку план с чересчур мелкой гнездовой выборкой отрицательно влияет на надежность данных (формирование кластеров рассматривается в разделе 3.3.5). Размер выборки должен учитывать противоречащие друг другу потребности, с тем чтобы были оптимально сбалансированы уровни затрат и точность собираемых данных. Размер выборки должен также соответствовать насущным потребностям пользователей, желающих получить данные по областям обследования, а именно – по подгруппам населения или небольшим районам. План выборки должен предусматривать достижение максимальной точности двумя основными способами: во-первых, используемый (или формируемый) инструментарий выборки должен быть как можно более полным, точным и обновленным и, во-вторых, должны использоваться такие методы формирования выборки, которые сводят к минимуму непреднамеренные погрешности, которые иногда допускаются ее составителями. План выборки также должен поддаваться самооценке, иными словами план выборки должен быть таким, чтобы ошибки выборки могли быть оценены и давали возможность пользователям рассчитывать надежность основных результатов обследования. Ошибки выборки возникают в результате оценки характеристик той или иной совокупности, базирующихся на данных только о ее части, а не обо всей совокупности в целом.

4. Основной целью любого обследования является возможность делать заключения касательно исследуемой совокупности, базируясь на случайной выборке. Для достижения этой цели исследователь обычно стремится оценить некоторые неизвестные характеристики совокупности. В число общих подлежащих оценке характеристик/параметров совокупности входят суммарные величины, средние величины, соотношения и вариантности. Например, если Y1, Y2, Y3 … … YN являются значениями переменной у в совокупности, тогда

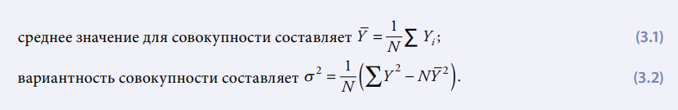
В большинстве случаев оценки выборки используются и для оценки параметров совокупности. Например, среднее значение и вариантность выборки размера n для простой случайной выборки с замещением рассчитываются по формулам:

где у1, y2, у3, ... ... yn – это значения переменной у для n числа единиц в выборке. В выборочных обследованиях исследователи рассчитывают вариантность отдельных случайных переменных для определения значения ошибки выборки в полученной оценке (см. определение ошибки выборки в таблице 3.1, более подробно ошибки выборки рассматриваются в главе 7 и приложении I). К факторам, влияющим на размеры вариантности выборки, относятся: однородность исследуемых переменных, размер выборки и план выборки (эти аспекты рассмотрены в различных разделах данной главы, главы 7, а основные принципы формирования выборки обследования представлены в приложении I).
5. В главах 3 и 4 подробно рассматривается каждый из параметров, используемых при формировании надлежащей выборки для обследований домашних хозяйств. Как правило, речь в основном идет о национальных обследованиях, хотя все описанные здесь методы применимы и к крупным обследованиям на субнациональном уровне, например, ограниченным одним или несколькими регионами, провинциями, районами или городами. В силу огромной важности инструментария выборки для достижения приемлемых практических результатов в формировании выборки, глава 4 полностью посвящена этому вопросу.

3.1.2. Глоссарий терминов по выборке и связанным с ней областям

6. Мы начинаем с глоссария терминов, используемых в данной и последующих главах (см. таблицу 3.1). Этот глоссарий не предназначен для предоставления официальных определений терминов по выборке, частично относящихся к области математики. Вместо этого в нем дается описание терминов в контексте данного руководства, конечно, с упором на их применение в обследованиях домашних хозяйств.

Таблица 3.1. Глоссарий терминов по выборке и связанным с ней областям

3.1.3. Символы

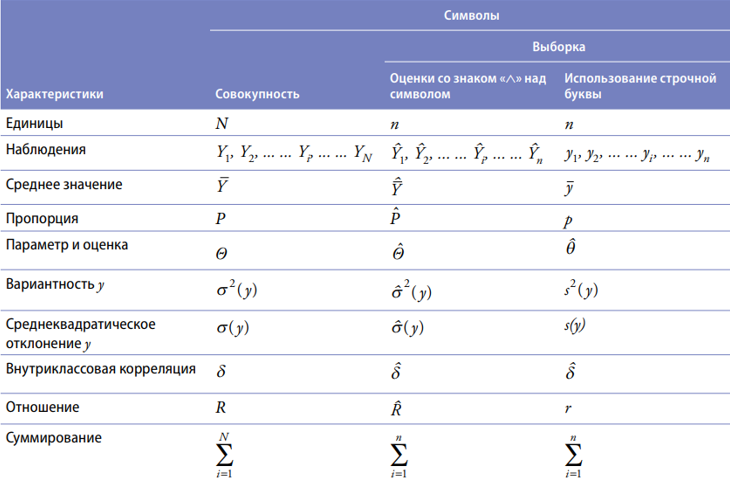
7. В этой и следующих главах настоящего руководства используются стандартные символы (см. таблицу 3.2). Как правило, прописные буквы обозначают величины совокупности, а строчные буквы обозначают наблюдения выборки. Например, символы Y1, Y2, Y3 … … YN обозначают величины совокупности, в то время как символы у1, y2, у3, ... ... yn обычно используются для указания выборочных значений. Из вышесказанного вытекает, что N — это размер совокупности, в то время как n обозначает размер выборки. Важно отметить, что параметры совокупности обозначаются либо прописными буквами английского алфавита, либо греческими буквами. Например, Ȳ и σ обозначают среднее значение и среднеквадратическое отклонение совокупности, соответственно. Оценки параметров совокупности имеют знак ^, расположенный над прописной буквой, например Ȳ, в то время как символ выборочных значений ȳ обозначается строчной буквой.

Таблица 3.2. Отдельные символы, используемые для обозначения величин совокупности и параметров выборки

3.2. Сравнение вероятностной выборки с другими методами выборки для обследований домашних хозяйств

8. Хотя обсуждение теории вероятностей лежит за рамками данного руководства, важно разъяснить, почему вероятностные методы играют незаменимую роль в формировании выборки для обследований домашних хозяйств. В данном разделе даются краткое определение и описание вероятностной выборки, а также излагаются причины, указывающие на важность этого параметра. Кратко упоминаются также другие методы, такие как выборка по экспертной оценке, или преднамеренная выборка, выборка путем случайного «блуждания», выборка по квотам и нерепрезентативная выборка, которые не удовлетворяют условиям вероятностной выборки, с изложением причин того, почему такие методы не рекомендуются для обследований домашних хозяйств.

3.2.1. Вероятностная выборка

9. Вероятностная выборка в контексте обследования домашних хозяйств включает средства, с помощью которых элементы обследуемой совокупности – территориальные единицы, домашние хозяйства и отдельные лица – отбираются для включения в обследование. Вероятностная выборка требует, чтобы: a) каждый элемент имел известную математическую вероятность быть отобранным, b) эта вероятность была выше нуля и с) эта вероятность была количественно рассчитана. Важно отметить, что вероятность отбора каждого элемента может быть не одинаковой, а варьироваться в соответствии с целями обследования.

10. Именно математическая природа вероятностной выборки позволяет получать по результатам обследования научно-обоснованные оценки. Более важно то, что она создает ту основу, на которой делаются умозаключения о том, что оценки выборки характеризуют всю совокупность, из которой получена данная выборка. Важнейшим побочным продуктом применения вероятностной выборки в обследованиях домашних хозяйств является то, что могут быть оценены ошибки выборки по данным, собранным на основе описываемых выборкой случаев. Ни один из указанных признаков не характерен для методов детерминированной выборки. В силу этих факторов настоятельно рекомендуется всегда использовать вероятностную выборку в обследованиях домашних хозяйств даже в том случае, если затраты на проведение обследования будут выше, чем в случае ненаучных, детерминированных методов.

3.2.1.1. Поэтапная вероятностная выборка

11. Из вышесказанного вытекает, что для выполнения обозначенных требований вероятностная выборка должна использоваться на каждом этапе процесса формирования выборки. Например, первый этап отбора, как правило, предусматривает отбор географически определенных единиц, таких как деревни. Последний этап предусматривает отбор конкретных домашних хозяйств или лиц для последующего опроса. Для формирования надлежащей выборки на этих двух этапах и на любых промежуточных этапах должны использоваться вероятностные методы. Ниже для иллюстрации приводится упрощенный пример.

Пример

Предположим, что простая случайная выборка (ПCB) из 10 деревень отобрана из общего числа в 100 деревень в одной сельской провинции. Предположим далее, что для каждой вошедшей в выборку деревни сделан полный список домашних хозяйств. Из этих списков для проведения опроса выполнен систематический отбор одного из каждых пяти домашних хозяйств, вне зависимости от того, сколько домашних хозяйств вошло в списки по каждой деревне. Это – двухэтапный план вероятностной выборки, при этом на первом этапе вероятность включения в выборку составляет 10/100, а на втором этапе – 1/5. Общая вероятность отбора конкретного домохозяйства для обследования составляет 1/50, т.е. отношение 10/100, умноженное на 1/5.

12. Не отличаясь особой эффективностью, указанный в этом примере план выборки, тем не менее, иллюстрирует то, каким образом на обоих этапах формирования выборки используется вероятностная выборка. В результате этого, оценка результатов обследования может проводиться без погрешностей путем надлежащего применения вероятностей отбора на этапе анализа данных в процессе проведения обследования (см. изложение проблемы взвешивания результатов обследования в главе 6).

3.2.1.2. Расчет вероятности

13. Приведенный выше пример также иллюстрирует, каким образом были удовлетворены два других требования к вероятностной выборке. Во-первых, каждой деревне в данной провинции придана отличная от нуля вероятность включения в выборку. В противном случае, если бы одна или более деревень были исключены из рассмотрения по любой причине, в том числе по соображениям безопасности, вероятность включения в выборку таких деревень была бы равна нулю, и, следовательно, вероятностный характер выборки был бы нарушен. Домашние хозяйства в приведенном выше примере также были отобраны с отличной от нуля вероятностью. Однако, если бы некоторые из них были целенаправленно исключены, например, в связи с их недоступностью, у них была бы равная нулю вероятность включения, и в этом случае осуществление выборки вернулось бы к детерминированному формату. В разделе 3.2.1.3 рассматриваются пути решения проблемы, возникающей, когда те или иные районы исключаются из обследования.

14. Во-вторых, вероятность включения в выборку как деревень, так и домашних хозяйств фактически может быть рассчитана на базе имеющейся информации. Применительно к отбору деревень были известны и размер выборки (10), и размер совокупности (100), и именно эти параметры определили вероятность, равную 10/100. Для домашних хозяйств расчет вероятности был несколько иным, поскольку до обследования нам не было известно, сколько домашних хозяйств должны быть отобраны в каждой из вошедших в выборку деревень. Нам было просто указано выбрать одно домохозяйств из пяти. Следовательно, если бы в деревне А было всего 100 домохозяйств, а в деревне В — 75, мы бы отобрали, соответственно, 20 и 15 из них. По-прежнему, вероятность отбора любого домохозяйства составляла бы 1/5 вне зависимости от размера совокупности и размера выборки (20/100 = 1/5, и так же для 15/75).

15. Вновь ссылаясь на приведенный выше пример, следует отметить, что вероятность отбора на втором этапе могла бы быть рассчитана путем перекрестной проверки после завершения обследования. Если известны величины m_iи М_i, где m_iи М_i представляют собой, соответственно, число домашних хозяйств в выборке и общее число домашних хозяйств в i-ой деревне, эта вероятность будет равна т_i/М_i. Всего таких вероятностей будет 10 – по одной для каждой деревни, включенной в выборку. Однако, как было отмечено, это соотношение для указанного плана выборки всегда будет равно 1/5. При этом было бы излишним делать подсчет выборки и общего числа домохозяйств с единственной целью – рассчитать вероятность для второго этапа. Тем не менее в целях контроля качества было бы полезно получить такие расчеты для обеспечения правильности применения доли выборки, равной 1 из 5.

3.2.1.З. Случаи, когда неправильно определена обследуемая совокупность

16. Иногда условия вероятностной выборки нарушаются по причине расплывчатости критериев определения обследуемой совокупности. Например, к предназначенной для обследования совокупности могут относиться все домашних хозяйств страны. Однако при составлении плана/проведении обследования из него зачастую преднамеренно исключаются определенные подгруппы населения, такие как кочевые домохозяйства, команды на судах, а также группы населения, проживающие в труднодоступных районах. В других случаях из обследуемой совокупности, предназначенной для охвата ограниченных, особых групп населения, таких как женщины, когда-либо состоявшие в браке, или молодежь в возрасте до 25 лет, по различным причинам исключаются важные по численности подгруппы. Например, из обследуемой совокупности, охватывающей молодежь в возрасте до 25 лет, могут исключаться лица, находящиеся на военной службе, или в заключении, или в иных специальных учреждениях.

17. В любом случае, когда фактическая обследуемая совокупность отличается от задуманной ранее, группа, проводящая обследование, должна уделить особое внимание более точному повторному определению обследуемой совокупности. Это представляется важным не только для разъяснения пользователям результатов обследования, но и для соответствия условиям вероятностной выборки. В указанном выше примере касательно молодежи в возрасте до 25 лет необходимо более точно описать и повторно определить обследуемую совокупность, как молодежь в возрасте до 25 лет, не находящуюся на военной службе или в специальных учреждениях. В противном случае сферу охвата обследования необходимо расширить путем включения в него указанных исключенных подгрупп.

18. Следовательно, важно весьма тщательно определять обследуемую совокупность, с тем чтобы она охватывала только такие единицы, которым фактически будет предоставлена вероятность быть отобранными для обследования. Совершенно очевидно, что в тех случаях, когда преднамеренно исключаются те или иные подгруппы, чрезвычайно важно применять вероятностные методы к фактической совокупности, составляющей инструментарий выборки. Более того, руководители обследования должны взять на себя обязанность четко разъяснить пользователям после опубликования результатов работы, какие сегменты населения включены в обследование, а какие – исключены из него.

3.2.2. Методы детерминированной выборки

19. В отличие от вероятностной выборки не существует статистической теории, которая бы лежала в основе использования детерминированной выборки. Она может оцениваться только субъективными методами. Отказ от использования вероятностных методов означает, таким образом, что оценки по результатам обследования будут иметь погрешность. Более того, масштаб таких погрешностей, а подчас и их направленность в сторону недооценки или переоценки будут неизвестны. Как указывалось выше, точность выборочных оценок, а иными словами, их среднеквадратическая ошибка, могут быть оценены с применением вероятностной выборки. Это необходимо пользователям для оценки надежности показателей обследования и для построения доверительных интервалов вокруг этих показателей. Имеющие погрешность оценки могут появляться при вероятностной выборке в определенных условиях, например в случае, когда возникает необходимость в соответствии обследуемой совокупности другим средствам контроля (более подробно данный вопрос рассматривается в главе 6).

20. Несмотря на отсутствие теоретического обоснования, детерминированная выборка зачастую используется в различных условиях и ситуациях. Практикующие ее специалисты обычно обосновывают это низкими затратами, удобством или даже сомнением группы, проводящей обследование, что «случайная» выборка может не быть достаточно репрезентативной для обследуемой совокупности. В контексте обследований домашних хозяйств мы дадим краткий обзор различных видов детерминированной выборки, в основном с помощью примеров, и укажем некоторые из причин, по которым их не следует использовать.

3.2.2.1. Выборка по экспертной оценке

21. Выборка по экспертной оценке представляет собой метод, полагающийся на ‹экспертов» при отборе элементов выборки. Ее сторонники утверждают, что этот метод устраняет возникающую при использовании методов рандомизации возможность формирования «плохой» или смещенной выборки, как, например, такой выборки, при которой все элементы выборки неудачно концентрируются, скажем, в северо-западном регионе.

Пример
В качестве примера выборки по экспертной оценке при обследовании домашних хозяйств можно привести группу экспертов, которые целенаправленно отобрали географические районы в качестве элементов на первом этапе отбора в плане выборки и которые обосновали свое решение тем мнением, что данные районы являются типичными или репрезентативными в том или ином смысле или контексте.

22. Основной проблемой этого вида выборки является субъективность определения того, какой набор районов является репрезентативным. Как ни парадоксально, но этот выбор в значительной степени зависит от выбора самих экспертов. И наоборот, при применении вероятностной выборки эти районы будут сначала стратифицированы с использованием при необходимости любых критериев по желанию проектной группы. Следует отметить, что критерии стратификации могут даже быть субъективными, хотя существуют рекомендации по применению более объективных критериев (см. раздел 3.4 по вопросам стратификации). Тогда вероятностная выборка районов (отобранных одним из множества имеющихся способов) будет сформирована из каждой страты. Следует также отметить, что стратификация значительно снимает вероятность формирования смещенной выборки, подобной упомянутой выше. Именно по этой причине был изобретен метод стратификации. При стратифицированной выборке каждый район имеет известную, отличную от нуля вероятность отбора, которая является несмещенной и не подверженной субъективному мнению (даже в том случае, если сами страты будут определяться субъективно). С другой стороны, выборка по экспертной оценке не предусматривает ни механизма обеспечения отличной от нуля вероятности отбора для каждого района, ни механизма расчета вероятности отбора тех районов, которые в конечном счете включаются в выборку.

3.2.2.2. Выборка с помощью случайного «блуждания» или выборка по квотам

23. Другим широко используемым видом детерминированной выборки является так называемая процедура случайного «блуждания», осуществляемая на последнем этапе обследования домашних хозяйств. Этот метод зачастую применяется даже в том случае, если элементы выборки предыдущих этапов были отобраны с помощью надлежащих вероятностных методов. В приводимом ниже примере показан вид выборки, представляющий собой комбинацию выборки методом случайного блуждания и выборки по квотам. Последняя из них является еще одним методом детерминированной выборки, в которой регистраторам предоставляются квоты на опрос определенных категорий лиц.

Пример
В качестве иллюстрации этого метода регистраторам будут даны инструкции начать процесс опроса в некоторой произвольно выбранной географической точке, скажем, в деревне, и следовать по оговоренному маршруту для выбора подлежащих опросу домашних хозяйств. Инструкция может предусматривать выбор для опроса каждого n-гo домохозяйства или проверку каждого находящегося на маршруте домохозяйства на предмет наличия в нем представителей конкретной исследуемой группы населения, например детей младше 5 лет. В последнем случае в ходе обследования опрашивается каждое подпадающее под такой критерий домохозяйство вплоть до достижения какой-либо заранее определенной квоты.

24. Применение этой методологии зачастую обосновывается необходимостью избежать больших затрат средств и времени, понесенных на предыдущем этапе составления списка всех домашних хозяйств в районе выборки – деревне, кластере или сегменте – до отбора домохозяйств, подлежащих опросу. Ее использование также обосновывается возможностью избежать неполучения ответов, поскольку регистратор продолжает двигаться дальше от не давших ответы домохозяйств до тех пор, пока не наберет достаточное для выполнения квоты число ответивших домохозяйств. Кроме того, сторонники этого метода утверждают, что он остается не смещенным, если начальная точка маршрута выбирается на случайной основе. Они также утверждают, что есть возможность надлежащим образом рассчитать вероятности выбора, поделив отобранное число домохозяйств на общее число домохозяйств в данной деревне, исходя из того, что последний показатель либо известен, либо может быть достаточно точно оценен.

25. С учетом изложенных в предыдущем пункте условий, теоретически возможно получить вероятностную выборку. Однако на практике сомнительно когда-либо в действительности достичь этой цели. Такой подход обычно не работает в силу а) действий регистраторов и b) отношения к не ответившим домохозяйствам, включая те, которые могут потенциально войти в категорию не ответивших. Как показали многочисленные исследования, когда регистраторам предоставляются функции определять выборку на местах, результатом этого будет пристрастная выборка. Например, средний размер (число лиц) вошедших в выборку домашних хозяйств обычно бывает ниже, нежели число лиц, проживающих в этих домохозяйствах¹ . Исходя из свойств человеческой натуры, регистратор будет избегать опроса домохозяйства, в котором он, с его точки зрения, может столкнуться с какими-либо сложностями. По этой причине бывает проще обойти стороной домашнее хозяйство со злой собакой или то, которое находится за глухими воротами и выглядит недоступным, и выбрать вместо этого соседнее домохозяйство, с которым подобных проблем не возникает.

26. После замены не ответивших домохозяйств на ответившие выборка становится смещенной в сторону готовых к сотрудничеству и легко достижимых домохозяйств. Совершенно ясно, что имеют место различия в характеристиках домохозяйств в зависимости от их желания и готовности к участию в обследовании. При использовании метода выборки по квотам те лица, с которыми сложно войти в контакт или которые не хотят сотрудничать, будут с большой вероятностью недопредставлены в выборке по сравнению с вариантом использования вероятностной выборки. В последнем случае от регистраторов, как правило, требуют нескольких повторных посещений домохозяйств, члены которых временно отсутствуют. Более того, применительно к обследованиям, основанным на вероятностной выборке, регистраторов обычно готовят к использованию дополнительных мер для убеждения колеблющихся домохозяйств принять участие в опросе.

3.2.2.3. Нерепрезентативная выборка

27. Нерепрезентативная выборка также широко используется в силу простоты ее формирования. Хотя такая выборка и редко применяется в обследованиях домохозяйств, можно представить много примеров ее использования, скажем, при проведении обследования школьников старших классов в целенаправленно сформированной выборке школ, которые известны своей доступностью и готовностью к сотрудничеству, иными словами, «удобных». Другое, модное сейчас применение – это мгновенный опрос на Интернет-сайтах, когда заходящих на такие сайты пользователей просят высказать свое мнение по различным темам. Вполне очевидно, почему такая выборка является по своей сути смещенной и не должна использоваться для выводов по населению в целом.

3.3. Определение размера выборки для обследований домашних хозяйств

28. Данный раздел носит весьма детальный характер в силу важности определения размера выборки для всех операций и затрат в ходе обследования. Размер выборки важен не только с точки зрения того, какое число домашних хозяйств будет опрошено, но также и в плане того, сколько первичных единиц выборки (ПEB) из географических районов вошли в выборку, сколько надо привлечь регистраторов, насколько большой объем работы будет приходиться на одного регистратора и т.д. Существует множество факторов и параметров, которые необходимо учитывать при определении размера выборки, однако все они в значительной мере касаются целей измерения в рамках конкретного обследования. Мы рассмотрим проблему определения размера выборки по следующим аспектам: основные оценки, которые требуется получить, обследуемые совокупности, число домохозяйств, которые должны войти в выборку для оценки соответствующих обследуемых совокупностей, требуемая точность и доверительная вероятность, области оценки, необходимость измерения уровня того или иного показателя или его изменения, формирование кластеров, допуск на неполучение ответов и имеющийся бюджет. Совершенно очевидно, что размер выборки – это ключевой фактор, определяющий общий план выборки.

3.3.1. Числовые значения оценок обследования

29. В обследованиях домашних хозяйств как общей направленности, так и посвященных определенной теме, такой как здравоохранение или экономическая активность, каждая оценка (часто называемая показателем), которую необходимо получить из обследования, требует разных размеров выборки для надежного измерения. Размер выборки зависит от величины оценки, т.е. от ее ожидаемой доли в генеральной совокупности. Например, для надежной оценки доли домашних хозяйств, имеющих доступ к безопасной воде, требуется иной размер выборки, чем для оценки доли взрослого, не работающего на данный момент населения.

30. Выражения для расчета размеров выборки базируются на вероятностных предположениях, что истинный параметр совокупности находится в интервале с данной вероятностью (доверительная вероятность). Ширина (или точность) этого интервала зависит от значения вариантности совокупности, указанной в таблице 3.2, а также от доверительного уровня и от размера выборки. Как правило, чем выше однородность совокупности или желаемая доверительная вероятность, тем шире будет такой интервал. С другой стороны, ширина интервала будет сокращаться по мере увеличения размера выборки. Примеры доверительных интервалов приводятся в пункте 22 главы 7. Указанное ниже выражение определяет доверительный интервал среднего значения Ȳ совокупности, принимая во внимание оценку среднего значения Ȳ совокупности, базирующуюся на простой случайной выборке без замещения, имеющей размер n.

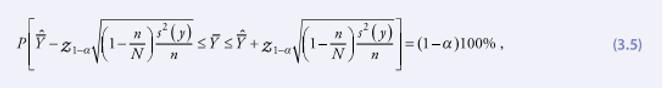
где 1 – α – это доверительный коэффициент для данного интервала. Следует отметить также, что применительно к оценке соотношения р, значение σ²(у)= р(1 – р).

31. На практике обследование само по себе может иметь только один размер выборки. Для расчета размера выборки необходимо сделать выбор среди многих оценок, которые должны быть получены в ходе того или иного обследования. Например, если ключевой оценкой является уровень безработицы, расчет размера выборки должен базироваться именно на нем². При наличии многих ключевых показателей иногда используется методика, по которой рассчитывается размер выборки, необходимый для каждого из них, а затем используется тот, который дает самую крупную по размеру выборку. Как правило, таким оказывается показатель, для которого базовая совокупность представляет собой наименьшую «подгруппу обследуемой совокупности» с точки зрения ее доли в генеральной совокупности. Необходимо, конечно, принимать во внимание желаемый уровень точности (см. ниже). Когда размер выборки базируется на такой оценке, каждая из прочих ключевых оценок будет измеряться с тем же или более высоким уровнем надежности.

32. В качестве альтернативы размер выборки может базироваться на сравнительно малой доле обследуемой совокупности вместо выделения какого-то определенного показателя. Это, по всей видимости, является наилучшим подходом для общих обследований домашних хозяйств, в которых упор делается на несколько не связанных друг с другом тем, и в этом случае может оказаться непрактичным или нецелесообразным базирование размера выборки на том или ином показателе, относящемся к какой-либо одной теме. Таким образом, руководители обследования могут принять решение при определении размера выборки исходить из возможности надежного измерения характеристик для 5 процентов (или 10 процентов) совокупности, при этом конкретный выбор будет зависеть от бюджетных соображений.

3.3.2. Обследуемая совокупность

33. Размер выборки также зависит от изучаемой совокупности, которая будет охватываться обследованием. Как и в случае с показателями, в обследованиях домашних хозяйств часто присутствует несколько изучаемых групп населения. Например, обследование в сфере здравоохранения может быть нацелено на а) домашние хозяйства для оценки их доступа к безопасной воде и санитарно-техническим системам, охватывая в то же время, b) всех лиц для оценки хронических и тяжелых нарушений здоровья, с) женщин в возрасте 14–49 лет для выявления показателей их репродуктивного здоровья и d) детей в возрасте до 5 лет для антропометрических измерений роста и веса.

34. Следовательно, необходимо рассмотреть размер выборки для каждой из этих исследуемых групп населения. Как указано выше, обследования домашних хозяйств зачастую включают несколько изучаемых совокупностей, каждая из которых представляет одинаковый интерес, с точки зрения целей обследования, в плане измерения тех или иных показателей. И вновь здесь имеет смысл сконцентрироваться на наименьшей совокупности для определения размера выборки. Например, если важнейшей целевой группой обследования являются дети младше 5 лет, размер выборки должен базироваться именно на этой группе. Применяя подход, описанный в пункте 32, руководящая группа по проведению обследования может принять решение по расчету размера выборки для оценки характеристики в отношении 10 процентов детей в возрасте до 5 лет. Полученный в результате размер выборки будет значительно больше, чем необходимо для целевой группы, состоящей из всех лиц, проживающих во всех домохозяйствах.

3.3.3. Точность и статистическая достоверность

35. Выше было приведено соображение о том, что оценки, особенно применительно к ключевым показателям, должны быть надежными. Определение размера выборки в значительной мере зависит от желаемого уровня точности показателей. Чем более точными или надежными должны быть результаты обследования, тем больше (на порядки величины) должен быть размер выборки. Например, удвоение требования надежности может обусловить необходимость увеличения размера выборки в четыре раза. Безусловно, руководители обследования должны быть осведомлены о том влиянии, которое оказывают чрезмерно строгие требования к точности на размер выборки и, следовательно, на уровень затрат при проведении обследования. И наоборот, они должны тщательно избегать слишком малых размеров выборки, в результате чего основные показатели будут слишком ненадежными для информативного анализа или эффективного планирования.

36. Аналогичным образом размер выборки увеличивается по мере роста желаемого уровня статистической достоверности для сохранения определенной точности. В качестве стандарта практически повсеместно принимается 95-процентный уровень доверительной вероятности, и соответствующим образом рассчитывается необходимый для достижения этого уровня размер выборки (см. пункт 30, выше).

37. Принимая во внимание те или иные показатели, методикой многих хорошо спланированных обследований является использование в качестве требуемого уровня точности предельного уровня относительной ошибки в 10 процентов при 95-процентном уровне доверительной вероятности по подлежащим измерению ключевым показателям, и это по сути означает, что среднеквадратическая ошибка того или иного ключевого показателя не должна превышать 5 процентов от самой оценки. Это рассчитывается, как (2 * 0,05х, где х – это оценка в ходе обследования). Например, если прогнозируемая доля населения в составе рабочей силы составляет 65 процентов, ее среднеквадратическая ошибка не должна превышать 3,25 процентных пункта, т.е. значение 0,65, умноженное на 0,05. Значение 0,0325, помноженное на два, или 0,065 дает предельный уровень относительной ошибки при 95-процентной доверительной вероятности. Например, как указано в пункте 30, выше, мы имеем:

38. Размер выборки, необходимый для достижения критерия, равного 10-процентному предельному уровню относительной ошибки, таким образом, представляет собой одну четвертую единицы, где предельный уровень относительной ошибки установлен на уровне 5 процентов. Предельный уровень относительной ошибки в 20 процентов обычно считается максимально допустимым для важных показателей (хотя мы не рекомендуем такой уровень). Это обусловлено тем, что доверительный интервал применительно к оценкам с более высокими допусками на ошибку слишком широк для получения содержательных результатов для большинства аналитических или стратегических целей. Как правило, при наличии соответствующего бюджета, мы рекомендуем предельный уровень относительной ошибки в 5–10 процентов в отношении основных показателей.

3.3.4. Группы анализа: области обследования

39. Еще одним существенным фактором, оказывающим большое влияние на размер выборки, является число областей обследования. Области обследования, как правило, определяются как аналитические подгруппы, для которых необходимы равнозначно надежные данные. Размер выборки увеличивается приблизительно³ на множитель, равный числу искомых областей обследования. Это, однако, является справедливым, если каждая из областей обследования демонстрирует аналогичный уровень изменчивости (для дополнительного разъяснения см. сноску 3).

Это происходит потому, что размер выборки для данного уровня точности не зависит от размера самой совокупности, за исключением случаев, когда размер выборки составляет существенную процентную долю совокупности – например 5 и более процентов (что редко встречается в случае обследований домашних хозяйств). Следовательно, размер выборки, требуемый для одной провинции (если обследование ограничено только одной провинцией), будет таким же, какой необходим для всей страны в целом. Это чрезвычайно важный момент, который зачастую неправильно понимается специалистами-практиками по проведению обследований, которые ошибочно полагают, что чем крупнее совокупность, тем больше должен быть размер выборки.

40. Таким образом, когда требуются лишь данные на национальном уровне, существует единственная область обследования, и соответствующим образом рассчитанный размер выборки применяется для выборки по всей стране в целом. Однако если принято решение о том, что результаты одинаковой надежности необходимо получить по городским и сельским районам по отдельности, то тогда требуемые размеры выборки будут рассчитаны для каждой области обследования в целях получения надежных результатов. Как правило, размер выборки для каждой из соответствующих областей обследования должен рассчитываться таким образом, что если будет D₁, D₂, ... ... D_к областей обследования, то обязательно будет n₁, n₂, … … n_k размеров выборки, которые будут зависеть от изменчивости соответствующих характеристик каждой из областей обследования, а также от установленных уровней доверительной вероятности и точности. Таким образом, общий размер выборки для всего обследования будет равняться n = n₁ + n₂ + + n_k.

3.3.4.1. Дополнительная выборка для оценок по областям обследования

41. Важным следствием требования равной надежности для областей обследования является необходимость использования непропорциональных долей выборки. Таким образом, когда распределение отклоняется от соотношения 50-50, что весьма вероятно для городских и сельских областей обследования, по всей видимости, в большинстве стран возникнет необходимость в применении преднамеренной дополнительной выборки, например, в городском секторе для достижения равной надежности. При этом следует подчеркнуть, что дополнительная выборка в той или иной области изучения в ходе общенационального обследования в основном диктуется необходимостью получения результатов с определенным доверительным уровнем.

42. Важно отметить два последствия применения преднамеренной дополнительной выборки в отношении подгрупп, как в областях, так и в стратах обследования. Во-первых, она требует применения в рамках обследования компенсирующих весовых коэффициентов для получения оценок на национальном уровне. Во-вторых, и что более важно, национальные оценки будут несколько менее надежными, чем они были бы в случае пропорционального распределения выборки среди подгрупп.

3.3.4.2. Отбор областей обследования

43. Подразделения территориальных единиц, безусловно, важны, и всегда существует соблазн рассматривать их в качестве областей обследования для целей получения соответствующих оценок. Например, при проведении общенационального обследования пользователи данных во властных структурах хотят получить данные не только по каждому крупному региону, но и зачастую по каждой провинции. Совершенно очевидно, что необходимо внимательно подойти к вопросу о числе областей обследования и обоснованно выбрать вид групп оцениваемых показателей, характеризующих данные области. Одной из приемлемых здесь стратегий является принятие решения о том, какие группы оценок, вне зависимости от их важности, требуют равнозначной надежности измерений в рамках обследования. Вместо этого группы оценок будут при анализе рассматриваться в качестве основных составных категорий таблиц, а не областей обследования. В этом случае размеры выборки для каждой такой категории будут меньше, чем если бы они рассматривались в качестве областей обследования; вследствие этого более низкой будет также и их надежность. При этом, однако, следует отметить, что дополнительная выборка в какой-либо определенной области обследования может быть обусловлена необходимостью получения оценок по данной области с определенными уровнями доверительной вероятности и точности вне зависимости от соответствующих уровней, установленных на национальном уровне.

Пример
Следующий пример показывает, каким образом будет сделана выборка и каково будет ее влияние на надежность оценок, если городские и сельские районы будут рассматриваться как группы категорий таблицы, а не как области обследования. Предположим, что распределение населения составляет: 60 процентов – сельское население и 40 процентов – городское. Если для удовлетворения оговоренного требования точности расчетный размер выборки был определен на уровне 8000 домашних хозяйств, то в случае, если городские и сельские районы устанавливаются как отдельные области обследования, 16 000 из них должны войти в такую выборку – по 8000 домохозяйств в каждом секторе. Вместо этого, рассматривая их в качестве групп в таблице, будет сформирована национальная выборка в количестве 8000 домохозяйств в соответствующей пропорции из городских и сельских районов, что дает, соответственно, 4800 и 3200 домохозяйств. Предположим далее, что ожидаемая среднеквадратическая ошибка для 10-процентной характеристики, базирующейся на выборке из 8000 единиц, составит 0,7 процентных пункта. Эта среднеквадратическая ошибка применяется в отношении оценки на национальном уровне (или в отношении городских и сельских районов по отдельности, если по каждой области обследования в выборку включены по 8000 домохозяйств). Для национальной выборки в 8000 домохозяйств, пропорционально сформированной из городских и сельских районов, соответствующая среднеквадратическая ошибка для сельских районов составит примерно 0,9 процентных пункта, при ее расчете как произведения квадратного корня отношения размеров выборки на среднеквадратическую ошибку национальной оценки, или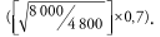

Для городских районов среднеквадратическая ошибка составит примерно 1,1 процентных пункта, или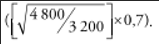

Другим способом этот эффект можно оценить, исходя из того факта, что среднеквадратические ошибки для всех сельских оценок будут примерно на 29 процентов выше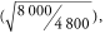

чем для национальных оценок; для городских районов они будут примерно на 58 процентов выше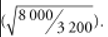

44. Следует отметить, что последнее суждение в вышеуказанном примере применимо вне зависимости от того, какая среднеквадратическая ошибка установлена на национальном уровне. Иными словами, оно применимо к любой оценке, включенной в таблицу обследования. Следовательно, появляется возможность анализа влияния на надежность данных еще до формирования выборки для различных подгрупп, которые могут рассматриваться в качестве областей обследования. Используя такой подход, группа по проведению обследования будет располагать информацией, которая поможет ей принять решение о том, следует ли рассматривать потенциальные области обследования в качестве групп таблицы. Как следует из вышесказанного, это означает, что надлежит использовать пропорциональное, а не равное распределение выборки. Например, если общенациональное обследование планируется в стране, имеющей только 20 процентов городского населения, размер выборки для городских районов будет составлять лишь 20 процентов от общего размера выборки. Следовательно, ошибка выборки для городских оценок будет в два раза (квадратный корень из 0,8n/0,2n) превышать ошибку выборки для сельских оценок и примерно в два с четвертью раза (квадратный корень из n/0,2n) превышать ошибку выборки для национальных оценок. В этом случае руководители обследования могут принять решение о необходимости дополнительной выборки в городском секторе⁴, создавая, таким образом, отдельные городские и сельские области обследования.

45. Аналогичным образом можно проанализировать взаимосвязь между среднеквадратическими ошибками и областями обследования по сравнению с группами таблицы для помощи в принятии решения о том, стоит ли использовать регионы или другие субнациональные административные единицы в качестве областей обследования, и если да – то какое их количество следует использовать. При равных размерах выборки, необходимых для областей обследования, использование 10 регионов потребует выборку в 10 раз больше размера национальной выборки, однако этот размер сократится вдвое, если будет признано, что лишь пять регионов достаточно отобрать для выполнения стратегических целей. Аналогичным образом, если вместо этого регионы будут рассматриваться как группы таблицы, национальная выборка будет распределена между ними пропорционально. В этом случае средний регион будет иметь среднеквадратическую ошибку примерно в 3,2 раза выше, чем национальные оценки в случае 10 регионов, и только в два раза выше – в случае пяти регионов.

3.3.5. Влияние гнездовой группировки

46. В данном разделе рассматривается вопрос о том, каким образом формирование кластеров влияет на размер выборки (более подробно проблема гнездовой выборки рассматривается в разделе 3.5). Та степень, в которой выборка обследования домашних хозяйств структурирована по кластерам, влияет на надежность или точность оценок, а следовательно, и на размер выборки. Влияние гнездовой группировки при обследовании домашних хозяйств возникает из-за а) предпоследних единиц выборки, обычно называемых «кластерами», в качестве которых могут выступать деревни или городские микрорайоны, b) вошедших в выборку домохозяйств, с) размера и/или изменчивости кластеров и d) метода включения в выборку домохозяйств в рамках отдельных кластеров. Влияние гнездовой группировки, а также стратификации может быть численно измерено с помощью эффекта схемы или deff, который является выражением того, насколько возрастает вариантность выборки (квадрат среднеквадратической ошибки) для стратифицированной гнездовой выборки по сравнению с простой случайной выборкой такого же размера. Стратификация склонна снимать вариантность выборки, однако лишь незначительно. И наоборот, гнездовая группировка значительно увеличивает вариантность. Таким образом, deff в основном показывает, в каком объеме гнездовая группировка присутствует в выборке обследования.

47. Эффективный план выборки требует использования кластеров для снижения затрат при одновременном сохранении эффекта схемы на низком по возможности уровне для того, чтобы результаты обследования были пригодными к использованию и надежными. К сожалению, величина deff не известна до проведения обследования и может быть оценена только по его итогам из самих данных. В случаях, когда проводились предыдущие обследования или аналогичные обследования в других странах, величины deff таких обследований можно использовать в качестве косвенных показателей в формуле расчета для оценки размера выборки.

48. Для сохранения эффекта схемы на низком по возможности уровне план выборки должен следовать следующим общим принципам (см. также краткие рекомендации в конце данной главы):

а) использование максимального практически возможного числа кластеров;

b) использование наименьшего практически возможного размера кластеров с точки зрения числа домохозяйств; 

с) использование постоянного, а не переменного размера кластеров;

d) формирование на последнем этапе систематической выборки домохозяйств, которые географически разбросаны, а не сегмента территориально прилегающих друг к другу домохозяйств

49. Таким образом, для выборки в 12 000 домохозяйств предпочтительно сформировать 600 кластеров по 20 домохозяйств в каждом, чем 400 кластеров по 30 домохозяйств в каждом. В первом случае эффект схемы выборки будет значительно меньше. Более того, величина deff снижается, если из всех домохозяйств одного кластера домохозяйства отбираются систематически, а не из территориально прилегающих друг к другу подсегментов. При соблюдении этих эмпирических правил эффект схемы будет оставаться в разумно низких пределах.

3.3.6. Поправка на прогнозируемое неполучение ответов при определении размера выборки

50. Общепринятой практикой при проведении обследований является увеличение размера выборки на величину, равную прогнозируемой доле неполучения ответов. Это обеспечивает то, что фактическое число опросов, проведенных в рамках обследования, будет приблизительно соответствовать целевому размеру выборки.

51. Показатели неполучения ответов в обследованиях широко варьируются по различным странам и видам обследований. В проведенных ниже расчетах мы исходим из предполагаемой доли неполучения ответов на уровне 10 процентов. Безусловно, любая страна должна использовать цифру, которая наиболее точно отражает опыт последних национальных обследований.

3.3.7. Размер выборки для эталонных выборок

52. Эталонные выборки подробно рассматриваются в главе 4. В данном разделе упор делается на размере выборки для плана эталонной выборки. Вкратце, эталонная выборка – это крупная выборка ПEB для тех стран, которые осуществляют крупномасштабные и непрерывные комплексные программы обследований. Такая крупная выборка предназначена для предоставления достаточного числа «зарезервированных» типов выборки в целях поддержки проведения многочисленных обследований в течение нескольких лет без необходимости многократного опроса одних и тех же респондентов.

53. В условиях, когда многочисленные обследования и, следовательно, многочисленные темы охвачены эталонной выборкой, безусловно, существуют и многочисленные изучаемые совокупности, которые должны быть обследованы, и ключевые оценки, которые должны быть получены. В этой связи большинство стран формируют размер выборки, исходя из двух соображений. Во-первых, и это само собой разумеется, присутствуют бюджетные соображения. Во-вторых, это – предполагаемые и охватываемые эталонной выборкой размеры выборки отдельных обследований, которые могут использоваться в течение определенного периода времени, часто вплоть до 10 лет между переписями населения. Следовательно, возможные размеры выборки для эталонных выборок доходят до весьма крупных размеров, достигая 50 000 домашних хозяйств и более. Тщательно отработаны планы применения всего архива домашних хозяйств.

Пример

Предположим, что эталонная выборка страны А состоит из 50 000 домашних хозяйств. Эталонную выборку предполагается использовать в трех уже запланированных обследованиях, а также, возможно, в двух других, которые еще не запланированы. Одно из обследований касается вопроса доходов и расходов домохозяйств и должно повторяться три раза в течение десяти лет – в 1-й, 5-й и 8-й годы. В рамках каждого из трех этапов этого обследования запланирован опрос 5000 домохозяйств. На 5-м году, однако, предполагается заменить в выборке 4 000 домохозяйств, т. е. половину из 8000 домохозяйств, опрошенных в 1-й год. Аналогичным образом, на 8-й год будут заменены на новые оставшиеся от 1-гo года 4 000 домохозяйств. Таким образом, для обследования доходов и расходов будет использовано 16 000 домохозяйств. Второе запланированное обследование проводится по теме здравоохранения, в котором, как ожидается, будет использовано около 10 000 домохозяйств, а в третьем обследовании рабочей силы будет использовано примерно 12 000 домохозяйств. Суммарно 38 000 домашних хозяйств будет зарезервировано для этих трех обследований. Соответственно, 12 000 домохозяйств все еще остаются неохваченными и могут быть при необходимости использованы для других обследований.

3.3.8. Оценка изменений или уровня показателей

54. Основной целью измерений, которые проводятся в рамках обследований на периодической основе, является оценка изменений, происшедших в период между обследованиями. По статистической терминологии, оценка, полученная при первом обследовании, представляет уровень того или иного показателя, в то время как разница между этим уровнем и оценкой уровня, полученной во втором обследовании, является расчетным изменением. Как правило, для оценки изменения в целях получения надежных выводов требуется значительно более крупный размер выборки, чем необходимый для оценки одного лишь уровня. Этот особенно справедливо при измерении небольших изменений. При этом, однако, существует ряд методов формирования выборки, предназначенных для сокращения размера выборки (и, следовательно, затрат на обследование) при оценке изменений (см. раздел 3.9.2). 

3.3.9. Бюджет обследования

55. Само собой разумеется, что при определении надлежащего размера выборки для обследования домашних хозяйств нельзя игнорировать бюджет обследования. Хотя бюджет не является числовым параметром в математическом расчете размера выборки, он играет заметную роль на практическом уровне.

56. Первоначальными расчетами размера выборки занимаются статистики, которые учитывают каждый параметр, рассматриваемый в данной главе. При этом довольно часто такой размер оказывается больше, чем может обеспечить бюджет обследования. Когда это происходит, группа по проведению обследования должна либо просить дополнительное финансирование обследования, либо вносить изменения в свои цели измерений, снижая требования к их точности или число областей обследования.

57. В функции технического специалиста по формированию выборки входит оказание помощи в ходе обсуждения зависимости «затраты–точность». Такой специалист должен разъяснить баланс соображений, возникающих в связи с ограничением числа областей обследования (меньше практических выгод для пользователей данных) или снижением требований к точности измерений (снижение надежности ключевых показателей) во всех случаях, когда возникает необходимость сокращения надлежащего размера выборки в связи с бюджетными возможностями. Такое обсуждение должно проводиться с применением примеров по точности оценок и областям обследования, приведенных выше. Давая рекомендации группе по проведению обследования, специалист по выборке должен внимательно учитывать и тот факт, что число кластеров также является ключевым определяющим фактором расходов на обследование (этот вопрос дополнительно рассматривается в разделе 3.5.5).

3.3.10. Расчет размера выборки

58. В данном разделе мы представляем формулу расчета размера выборки, принимая во внимание рассмотренные выше параметры. В связи с тем, что основной упор мы делаем на обследованиях домашних хозяйств, размер выборки рассчитывается в плане численности подлежащих отбору домашних хозяйств. Приведен также ряд примеров.

59. Как правило, когда включено соотношение р, формула расчета размера выборки, n_b, является следующей⁵:

где n_b – это искомый параметр размера выборки в плане численности подлежащих отбору домашних хозяйств; z – статистическая величина, определяющая желаемую доверительную вероятность; r – величина ключевого показателя, подлежащего измерению в рамках обследования; f – эффект схемы выборки, deff, принимаемый равным 2,0 (значение по умолчанию); k – множитель, необходимый для учета предполагаемой доли неполучения ответов; р – доля генеральной совокупности, вошедшая в обследуемую совокупность и на которой базируется параметр r, ň –средний размер домашнего хозяйств (число лиц, проживающих в домохозяйстве); и е – допустимый предел ошибки, к которому следует стремиться. Ниже приводятся рекомендуемые значения некоторых параметров.

60. Предполагаемая к использованию статистическая величина z должна составлять 1,96 для 95-процентного уровня доверительной вероятности (по сравнению, например, со значением 1,645 для 90-процентного уровня). Первая величина обычно считается стандартом для придания желаемого уровня доверительной вероятности при оценке допустимого предела ошибки в обследованиях домашних хозяйств. Принимаемая по умолчанию величина эффекта схемы выборки обычно устанавливается на уровне 2,0, если не существует дополнительных эмпирических данных прошлых или аналогичных обследований, доказывающих иную величину. Поправочный множитель на неполучение ответов, k, должен выбираться таким образом, чтобы отражать собственный опыт конкретной страны в части неполучения ответов в обследованиях – обычно менее 10 процентов для развивающихся стран. Таким образом, осторожным подходом к множителю будет выбор его значения на уровне 1,1. Параметр р обычно может быть рассчитан, исходя из результатов последней переписи. Параметр ň зачастую составляет около 6,0 в большинстве развивающихся стран, однако его необходимую для использования в формуле точную величину обычно можно получить из последней переписи. Что касается допустимого предела ошибки, е, рекомендуется, чтобы уровень точности устанавливался равным 10 процентам от r; следовательно, е=0,10r. Меньший размер выборки может формироваться с менее строгим допустимым пределом ошибки, е=0,15r, однако в этом случае результаты обследования, безусловно, будут менее надежными. Подстановка в формулу выбранных величин дает следующий результат:

Уравнение (3.2) сокращает формулу до следующего вида:

61. Сокращенный вариант может использоваться в случаях, когда вместо более точных показателей, полученных на основании опыта конкретной страны, применяются все рекомендуемые по умолчанию значения указанных выше параметров.

Пример
В стране В принято решение, что основным искомым показателем обследования будет уровень безработицы, который предполагается равным примерно 10 процентам от численности трудоспособного гражданского населения. Трудоспособное гражданское население определяется как население в возрасте 14 лет и старше и составляет примерно 65 процентов от общей численности населения страны. В этом случае r = 0,1 и p = 0,65. Предположим, что, как рекомендовано выше, мы хотим оценить уровень безработицы с 10-процентным допустимым пределом относительной ошибки при 95-процентном уровне доверительной вероятности; в таком случае е = 0,10r (иными словами, среднеквадратическая ошибка составляет 0,01). Далее мы принимаем рекомендуемые значения ожидаемой доли неполучения ответов, эффекта схемы и среднего размера домашнего хозяйства. Тогда мы имеем право применить формулу (3.9), которая в итоге дает 1170 домашних хозяйств [(84,5x0,9)/(0,1x0,65)]. Это – сравнительно небольшой размер выборки, прежде всего в силу того, что базовая совокупность составляет большую долю от генеральной совокупности, а именно 65 процентов. Напомним, что искомый размер выборки рассчитывается для одной области обследования – в данном случае на национальном уровне. Если цели измерения предусматривают получение в равной степени надежных данных для городских и сельских районов, тогда размер выборки необходимо удвоить, исходя из того, что все параметры формул (3.8) и (3.9) применяются как для городских, так и для сельских районов. Чем больше они различаются (например, средний размер городских домохозяйств может отличаться от сельских домохозяйств, так же как могут отличаться ожидаемые доли неполучения ответов для городских и сельских районов), тем более точные величины необходимо использовать для отдельного расчета размеров выборки для городских и сельских районов. Результаты этих расчетов, безусловно, будут разными.

62. Приведенный ниже пример охватывает меньшую по размеру базовую совокупность – дети в возрасте до 5 лет.

Пример
В стране С в качестве основного показателя обследования определен уровень смертности среди детей в возрасте до 5 лет, который предполагается равным примерно 5 процентным пунктам. В этом случае r = 0,05, а р оценивается примерно в 0,15 или 0,03x5. И вновь мы хотим оценить уровень смертности с 10-процентным допустимым пределом относительной ошибки: тогда е =0,10r (или среднеквадратическая ошибка на уровне 0,005). Величины ожидаемой доли неполучения ответов, эффекта схемы и среднего размера домашнего хозяйства снова сохраняются на рекомендуемом нами уровне. Формула (3.9) дает около 10 704 домохозяйств (84,5x0,95)/(0,05x0,15), т.е. значительно более крупный размер выборки, чем в предыдущем примере. И опять основная причина этого связана с размером базовой совокупности, иными словами, детьми в возрасте до 5 лет, численность которых составляет лишь 15 процентов от генеральной совокупности. Оцениваемый размер параметра r также является небольшим, и этот факт в комбинации с небольшой величиной р вынуждают сформировать большой размер выборки.

63. Последний пример касается того случая, когда генеральная совокупность является обследуемой совокупностью. В этом случае р = 1 и может не учитываться; тем не менее здесь также можно применить формулы (3.8) и (3.9) при использовании рекомендованных величин, указанных выше параметров.

Пример
В стране D в качестве основного показателя обследования определена доля лиц в общем народонаселении, у которых в течение предшествующей недели возникли какие-либо острые заболевания. Эта доля оценивается на уровне между 5 и 10 процентами, и в этом случае будет использована меньшая величина, поскольку она даст более крупный размер выборки (консервативный подход). В этом случае r = 0,05, a p, естественно, равняется 1,0. Вновь мы хотим оценить уровень острых заболеваний с 10-процентным допустимым пределом относительной ошибки: е = 0,10r⁶ (или среднеквадратическая ошибка на уровне 0,005), а величины ожидаемой доли неполучения ответов, эффекта схемы и среднего размера домашнего хозяйства опять сохраняются на рекомендуемом нами уровне. Формула (3.9) в итоге дает чуть более 1600 домохозяйств (84,5x0,95)/(0,05).⁶

64. Как указывалось выше, размер выборки для обследования в конечном счете может определиться путем расчета размеров выборки для нескольких ключевых показателей и основывая выбор на том показателе, который дает наибольший размер выборки. Кроме того, до принятия окончательного решения необходимо также рассмотреть такие аспекты, как число областей обследования, а также бюджет обследования.
65. В тех странах, в которых не соблюдается одно или более из указанных выше допущений, в формуле (3.7) могут быть сделаны простые замены для получения более точных величин размера выборки. Например, средний размер домохозяйства может быть больше или меньше 6,0; доля неполучения ответов может прогнозироваться на уровне около 5 вместо 10 процентов, а величину для какой-либо конкретной страны, как правило, можно более точно рассчитать, используя результаты переписи.

66. Рекомендуется, однако, не вносить никаких изменений в величину статистического показателя z на уровне 1,96, который является общепризнанным стандартом. Из практических соображений также следует оставить на уровне 2,0 величину эффекта схемы, если только, как уже указывалось, результаты последней переписи из другого источника не дают иных данных. Рекомендуется также, чтобы величина е определялась как 0,10r, кроме тех случаев, когда имеющийся бюджет не может обеспечить расчетный размер выборки. В таком случае величина е может быть увеличена до 0,12r или до 0,15r. При этом такие увеличения в допустимом пределе ошибки дадут в итоге гораздо бoлee высокие ошибки выборки.

3.4. Стратификация

67. При планировании обследования домашних хозяйств широко применяемым методом является стратификация предполагаемой для обследования совокупности еще до формирования выборки. Она служит для целей классификации совокупности в подсовокупностях – стратах – на основе дополнительной информации, которая известна в отношении генеральной совокупности. Затем вне зависимости от каждой страты отбираются элементы выборки таким способом, который соответствует целям измерения в ходе обследования.

3.4.1. Стратификация и распределение выборки

68. В стратифицированной выборке размеры выборки в пределах каждой страты контролируются техническом специалистом по выборке, а не формируются путем случайного определения в процессе выборки. Разделенная на страты совокупность может иметь точно ns единиц, отобранных из каждой страты, где ns – это желаемое число единиц выборки в страте s. И наоборот, нестратифицированная выборка в итоге даст размер выборки для под совокупности в страте s, который будет несколько отличаться от ns.

Пример

Предположим, что план выборки обследования должен постоять из двух страт – городской и сельской. Из переписи населения имеется информация для разделения всех административно-территориальных единиц на городские или сельские, что позволяет стратифицировать население по данному критерию. Решено сформировать пропорциональную (в отличие от непропорциональной) выборку в каждой страте, поскольку население распределено в соотношении: 60 процентов – сельское население и 40 процентов – городское население. Если размер выборки составляет 5000 домохозяйств, независимое формирование выборки по стратам обеспечит, что 3000 из них будут сельскими и 2 000 – городскими. Если бы выборка формировалась произвольно без первоначальной стратификации, распределение домохозяйств в выборке отличалось бы от соотношения 3000 – 2 000, хотя такое распределение и было бы ожидаемым. Нестратифицированная выборка может для неудачного случая дать выборку в соотношении, скажем, 3 200 сельских домохозяйств и 1800 городских.

69. Таким образом, одной из причин стратификации является снижение шанса на неудачный вариант выборки и на наличие непропорционально большого (или небольшого) числа единиц выборки, отобранных из-под совокупности, которая считается показательной для анализа. Стратификация осуществляется для обеспечения надлежащей репрезентативности важных групп подсовокупности без внесения погрешностей в проводимый отбор. Важно, однако, отметить, что надлежащая репрезентативность не подразумевает пропорциональной выборки. Во многих случаях одна или более страт могут также являться областями оценки (как обсуждалось выше). В этом случае может возникнуть необходимость формирования выборки равного размера в используемых стратах, получая, таким образом, непропорциональную выборку по стратам. Следовательно, как пропорциональное, так и непропорциональное распределение единиц выборки среди различных страт является вполне допустимой особенностью стратифицированной выборки, и выбор зависит от целей измерения в рамках обследования.

70. Как подразумевалось в предыдущем абзаце, стратификация может также служить средством для неявного распределения выборки, что является более простым и практичным методом, чем оптимальное распределение⁷. Иными словами, при пропорциональной выборке по отдельные стратам нет необходимости заранее рассчитывать число единиц выборки, которые должны быть распределены по каждой страте.

Пример
Предположим, что цепью плана выборки является обеспечение точно пропорционального распределения общего размера выборки по каждой из 10 имеющихся в стране провинций. Если, скажем, в провинции А проживает 12 процентов населения страны, тогда в этой провинции должны быть отобраны 12 процентов кластеров выборки при условии, что ожидаемый размер выборки является постоянным. Предположим далее, что на национальном уровне необходимо выбрать всего 400 кластеров. Часто используемый во многих странах метод состоит в присвоении 45 (0,12 х 400) кластеров провинции А. Однако при надлежащей стратификации такая процедура становится ненужной. Вместо этого каждая провинция должна рассматриваться в качестве отдельной страты в процессе формирования выборки. Тогда применение систематической выборки с вероятностью, пропорциональной размеру (см. таблицу 3.1), с единым интервалом выборки автоматически приведет к искомым 48 кластерам в провинции А. Этот вид стратификации, а также возможности ее использования для упрощения схем распределения более подробно рассматриваются в разделе 3.4.3.

3.4.2. Правила стратификации

71. Существуют два базовых правила, которые применяются при стратификации какой-либо совокупности. Одно из правил необходимо соблюдать всегда. Обычно следует соблюдать и другое правило, хотя его несоблюдение не приведет к серьезному ущербу для плана выборки. Требуемое⁷ правило заключается в том, что по крайней мере одна единица выборки должна отбираться из каждой создаваемой страты. Страты являются по сути независимыми и взаимоисключающими подгруппами совокупности: каждый элемент совокупности должен присутствовать в одной и только в одной страте. В силу такой особенности каждая страта должна участвовать в выборке, с тем чтобы в выборку могла войти вся совокупность и была рассчитана несмещенная оценка совокупности. Поскольку каждая страта может теоретически рассматриваться независимо в плане выборки, нет необходимости создавать страты, используя объективные критерии; при желании могут применяться и субъективные критерии. Здесь применяется руководящий принцип, по которому формирующие ту или иную страту единицы должны быть в максимально возможной степени аналогичными в отношении переменных величин исследования для снижения вариантности в рамках каждой страты.

72. Вторым правилом стратификации является то, что каждая создаваемая страта должна в идеальном случае как можно больше отличаться от других. Следовательно, основным принципом формирования страт должна быть разнородность между стратами и однородность внутри страт. Таким образом, легко понять, почему городские и сельские районы зачастую формируются в качестве двух отдельных страт для обследования домашних хозяйств. Как указывалось выше, городское и сельское население отличается друг от друга по многим аспектам (вид занятости, источник и размер дохода, средний размер домохозяйства, уровень рождаемости и т.д.), в то время как лица, относящиеся к одной из этих подгрупп, обладают аналогичными характеристиками.

73. Однородность является полезным руководящим принципом для определения того, какое количество страт необходимо создать. Количество страт не должно превышать число поддающихся учету подгрупп населения в соответствии с определенным критерием, используемым для разграничения страт. Например, если какая-либо страна в административных целях разделена на восемь географических регионов, и при этом два из этих регионов весьма похожи друг на друга в отношении предмета предполагаемого обследования, надлежащий план выборки может быть достигнут путем создания семи страт (и объединяя два похожих региона). Никакого положительного эффекта не будет достигнуто в результате использования, например, 20 страт, если 10 из них могут предоставить одни и те же однородные подгруппы.

74. Важно отметить, что применительно к пропорциональному отбору результирующая выборка будет по крайней мере столь же точной, как простая случайная выборка такого же размера. Следовательно, стратификация дает повышение точности или надежности оценок обследования, при этом такое увеличение является максимальным в наиболее однородных стратах. Именно эта особенность стратифицированной выборки гарантирует, что даже неудачная стратификация⁸ не нанесет ущерба оценкам обследования с точки зрения их надежности.

75. Другой важный аспект касается оценки ошибок выборки. Хотя выбор одной единицы из каждой страты достаточен для выполнения теоретических требований стратифицированной выборки, необходимо отбирать как минимум две единицы для того, чтобы результаты выборки можно было использовать при расчете ошибок выборки в оценках обследования.

76. Иногда возникает необходимость использования многих переменных величин в целях стратификации. В таких случаях мы должны руководствоваться следующими факторами: предпочтительно, чтобы используемые для стратификации переменные величины были не связаны друг с другом, но при этом связаны с переменной величиной обследования; нет необходимости добиваться полной завершенности и при формировании ячеек (более мелкие и наименее важные ячейки могут объединяться); как правило, более заметного улучшения можно добиться путем использования более грубой разбивки многих переменных величин, чем более детальной разбивки одной переменной.

3.4.3. Неявная стратификация

77. Как указывалось выше, выбор имеющейся информации для создания страт зависит от целей измерения в ходе обследования. Для обследований домашних хозяйств, которые носят крупномасштабный и многоаспектный характер, особенно полезным методом является так называемая неявная стратификация. Тот факт, что ее важнейшим критерием являются географические особенности, как правило, служит достаточной основой для надлежащего распределения выборки по важным подгруппам населения, таким как городское и сельское население, административные регионы, этнические подгруппы, социально-экономические группы и т.д. В силу этого географического критерия неявная стратификация является весьма полезной даже тогда, когда предметом обследования служит единственная тема, например трудоспособное население, экономическая активность домашних хозяйств, измерение уровня бедности, здравоохранение или доходы и расходы. Этот метод настоятельно рекомендуется как по указанным выше причинам, так и в силу простоты его применения.

78. Для правильного применения неявная стратификация требует использования систематической выборки на первом этапе формирования выборки. Эта процедура проста в применении и предусматривает вначале расстановку файла ПEB в географической последовательности. Во многих странах такая последовательность, вероятнее всего, будет следующей: городское население в разбивке по провинциям и далее в пределах каждой провинции в разбивке по районам, затем сельское население в разбивке по провинциям и далее в пределах каждой провинции – по районам. Следующим шагом является систематический отбор ПEB из рассортированного файла. Систематической отбор производится либо путем равновероятностной выборки, либо, скорее всего, путем вероятностной выборки пропорционально размеру.

79. Как уже упоминалось, важным преимуществом неявной стратификации является то, что с ее помощью исключается необходимость в создании явных территориальных страт. Это, в свою очередь, устраняет необходимость распределять выборку между этими стратами, особенно при использовании пропорциональной выборки. Другим преимуществом является простота метода, рассмотренная в предыдущем пункте, поскольку этот метод требует всего лишь сортировки файла и применения надлежащего интервала(ов) выборки. Столь же легко можно применять непропорциональную выборку на первом уровне сортировки по географическому признаку. Например, если городское и сельское население представляет собой первый уровень, то достаточно понятной операцией выглядит применение различных долей выборки к городской и сельской частям населения. На рисунке 3.1 представлена схема неявной стратификации с систематической выборкой. Более подробно проблема формирования выборки с вероятностью пропорциональной размеру, рассматривается в разделе 3.6, ниже.

3.5. Гнездовая выборка

80. Изначально термин «гнездовая выборка» был введен для обозначения планов выборки, в которую входили все члены той или иной группы. Сами группы обозначались как кластеры или гнезда. Например, на первом этапе могла формироваться выборка школ, а на втором – классы. Если обследовались учащиеся каждого класса, тогда имелась гнездовая выборка классов. В обследованиях домашних хозяйств в качестве примера изначального понятия гнездовой выборки может служить отбор городских микрорайонов, в которых опросу в целях обследования подвергались все жители данного микрорайона. В последние годы, однако, термин «гнездовая выборка» широко используется для обозначения более общего плана обследований, имеющих предпоследний этап формирования выборки, для которой отбирались (и определялись) такие кластеры, как деревни, счетные участки переписи или городские микрорайоны. На последнем этапе формирования выборки проводится обследование не всех домохозяйств, а подгруппы выборки, состоящей из домохозяйств каждого отобранного кластера. Именно последний вариант применения данного термина, как правило, и используется в настоящем руководстве.

Рисунок 3.1. Распределение административных единиц в целях неявной стратификации

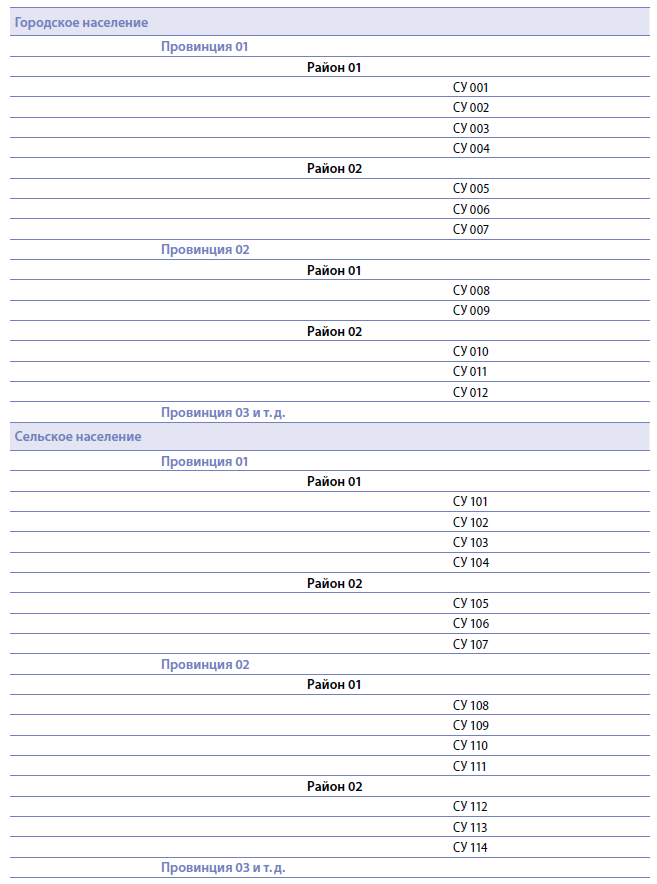
81. В обследованиях домашних хозяйств план выборки будет неизменно и по необходимости использовать ту или иную форму гнездовой выборки для сдерживания расходов на проведение обследования. Как указывалось выше, гораздо дешевле провести обследование, скажем, 1 000 домашних хозяйств по 50 адресам (20 домохозяйств на один кластер), чем 1000 домохозяйств, произвольно отобранных из всего населения. К сожалению, формирование кластеров выборки снимает надежность выборки в связи с высокой вероятностью того, что лица, проживающие в одном кластере, склонны к однородности или к обладанию более или менее аналогичными характеристиками. Этот так называемый эффект гнездовой группировки необходимо компенсировать в плане выборки путем соразмерного увеличения размера выборки.

3.5.1. Характеристики гнездовой выборки

82. Гнездовая выборка значительно отличается от стратифицированной выборки по двум аспектам⁹. Что касается последней – в выборке представлены все страты, поскольку единицы отбираются в выборку из каждой страты. В гнездовой выборке производится отбор самих кластеров, следовательно, вошедшие в выборку кластеры представляют не вошедшие кластеры. Это первое характерное различие между стратифицированной и гнездовой выборками обусловливает и второе их различие. Как указывалось выше, в идеальном случае страты должны создаваться таким образом, чтобы быть внутренне однородными при внешней разнородности в плане подлежащих измерению параметров обследования. Для кластеров справедливым является прямо противоположный подход. С точки зрения точности выборки, лучше, чтобы кластеры были по возможности внутренне разнородными.

83. Тот факт, что в обследованиях домашних хозяйств кластерами практически всегда являются территориальные единицы, такие как деревни или части деревень, к сожалению, означает, что, как правило, невозможно добиться высокой степени разнородности в пределах одного кластера. И действительно, географически определяемые кластеры с большой вероятностью будут внутренне однородными, чем разнородными, в плане таких переменных показателей, как вид занятости (например, фермерская деятельность), уровень дохода и так далее. Следовательно, степень однородности кластеров применительно к тому или иному переменному показателю определяет, насколько «подверженной гнездовой выборке» может быть та или иная выборка. Чем в большей степени гнездовая группировка присутствует в выборке, тем ниже ее надежность.

3.5.2. Эффект схемы применительно к кластеру

84. Эффект гнездовой группировки в выборке частично измеряется с помощью эффекта схемы (deff). Тем не менее deff также отражает эффекты стратификации. Группа по составлению плана выборки должна позаботиться о максимально возможном достижения в плане выборки оптимального баланса между минимизацией расходов и максимально возможной точностью данных. Это достигается, по мере возможности, путем сведения к минимуму или ограничения эффекта схемы. Для определения того, каким образом можно минимизировать или ограничить относящийся к гнездовой группировке элемент deff, полезно взглянуть на его математическое определение:

где δ – это внутриклассовая (или внутри кластерная) корреляция или, иными словами, та степень вероятности, с которой две единицы в кластере в сравнении с двумя единицами, произвольно отобранными из совокупности, будут иметь одно и то же значение; а ñ – это число единиц обследуемой совокупности в данном кластере.

85. Строго говоря, уравнение (3.10) не является формулой расчета для deff, поскольку в нем не учитывается стратификация, а также еще один фактор, который вводится в случае неоднородности кластеров по размеру. Тем не менее, поскольку относящийся к гнездовой группировке элемент является доминирующим фактором в величине deff, он может применяться в качестве приблизительной формы расчета, показывая, в какой степени гнездовая группировка воздействует на план выборки и что можно сделать для ограничения такого воздействия.

86. Из приведенного выше математического выражения можно увидеть, что deff – это мультипликативная функция двух переменных: внутриклассовой корреляции, δ, и размера кластера, ñ. Следовательно, значение deff возрастает при увеличении как δ, так и ñ. Хотя составитель выборки не может контролировать величину внутриклассовой корреляции для любой искомой переменной, он/она все же может при формировании выборки скорректировать размер кластера в сторону его увеличения или уменьшения и, таким образом, в значительной мере контролировать эффект схемы.

Пример
Предположим, что некая совокупность имеет внутриклассовую корреляцию, равную 0,03, что является достаточно малой величиной для случая хронических заболеваний. Предположим также, что планирующие выборку специалисты обсуждают, следует ли использовать кластеры из 10 или 20 домохозяйств при общем размере выборки в 5000 домохозяйств. Предположим далее, лишь для упрощения примера, что все домохозяйства имеют одинаковый по составу размер – пять человек. Тогда величина n будет равна 50 для 10 домохозяйств и 100 для 20 домохозяйств. Простая замена в уравнении (3.4) дает примерную величину deff [1 + 0,03(49)] или 2,5 для плана кластеров из 10 домохозяйств, но 4,0 – для плана кластеров из 20 домохозяйств. Следовательно, эффект схемы будет примерно на 60 процентов выше для более крупного размера кластера. Затем группа по проведению обследования должна решить, какой из двух вариантов лучше – включить в выборку в два раза больше кластеров (500), используя вариант с 10 домохозяйствами для сохранения надежности на более приемлемом уровне, или выбрать более дешевый вариант из 250 домохозяйств, заплатив за это значительным увеличением вариантности выборки. Безусловно, можно рассматривать и другие варианты в промежутке между 10 и 20 домохозяйствами.

87. Существует несколько путей интерпретации эффекта схемы: как множитель, на который вариантность фактического плана выборки, используемого (предполагаемого к использованию) в ходе обследования, превышает вариантность простой случайной выборки (ПCB) такого же размера; просто как измеритель того, насколько фактический план выборки хуже простой случайной выборки с точки зрения точности; или показатель, отражающий, сколько дополнительных единиц выборки необходимо отобрать в намечаемом плане выборки по сравнению с простой случайной выборкой для достижения такого же уровня вариантности выборки. Например, deff величиной в 2,0 означает, что необходимо удвоить число единиц, подлежащих выборке, для достижения такой же надежности, какую имеет простая случайная выборка. В связи с этим крайне нежелательно иметь план выборки со значениями deff, значительно превышающими 2,5–3,0 для ключевых показателей.

3.5.3. Размер кластера

88. Ранее было отмечено, что составитель выборки не может контролировать корреляцию. Кроме того, в отношении большинства переменных показателей обследования практически не существует эмпирических исследований, в которых делалась бы попытка оценки величины таких корреляций. Внутриклассовая корреляция теоретически может варьироваться в пределах от -1 до +1, хотя сложно представить себе переменные показатели по домашним хозяйствам, которые имели бы отрицательное значение. В связи с этим единственная возможность, которой располагает составитель выборки для сдерживания величины deff нa минимальном уровне, – это позаботиться о том, чтобы размеры кластеров были настолько малыми, насколько это позволяет бюджет. В таблице 3.3 указаны показатели deff для различных величин внутриклассовой корреляции и постоянного размера кластера.

89. Из таблицы 3.3 ясно видно, что размеры кластеров, превышающие 20, дают неприемлемые показатели deff (выше 3,0), если только при этом величина внутриклассовой корреляции не является весьма малой. При оценке цифр в таблице важно помнить, что ñ обозначает число единиц в обследуемой совокупности, а не число домохозяйств. В этой связи величина ñ, которая должна использоваться, равняется числу домохозяйств в кластере, помноженному на среднее число лиц в обследуемой группе населения. Если обследуемой группой являются, например, женщины в возрасте 14–49 лет, то обычно на одно домохозяйство приходится примерно одна женщина из такой группы, и в этом случае размер кластера из b домохозяйств будет иметь приблизительно такое же число женщин в возрасте 14–49 лет. Иными словами, значения ñ и b примерно равны для данной обследуемой группы, и таблица 3.3 применяется в данном неизменном виде. В следующем примере число домохозяйств и обследуемая совокупность в кластере не равны друг другу.

Таблица 3.3. Сравнение связанных с гнездовой группировкой элементов в эффекте схемы для различных величин внутриклассовой корреляции δ и размеров кластеров n

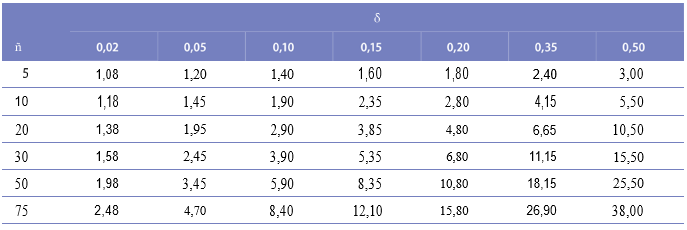
Пример
Предположим, что изучаемой совокупностью является все население, как это было бы в случае обследования состояния здравоохранения для оценки числа острых и хронических заболеваний. Предположим далее, что в этом обследовании планируется применять кластеры из 10 домашних хозяйств. В этом случае величина ñ будет в 10 раз больше размера среднего домохозяйства; если последний равен 5,0, то значение ñ будет равно 50. Следовательно, 50 – это величина ñ, которая должна использоваться в таблице 3.3 для оценки возможного значения deff. Таблица 3.3 показывает, что значение deff будет весьма высоким, кроме случаев, когда величина δ примерно равна 0,02. Это означает, что гнездовая выборка, в которой запланировано использование кластеров всего лишь из 10 домохозяйств, даст весьма ненадежные результаты для такой характеристики, как инфекционные заболевания, поскольку последний показатель будет, вероятнее всего, иметь большую величину δ.

90. Этот пример демонстрирует, почему столь важно учитывать размер выборки при планировании обследования домашних хозяйств, особенно в отношении ключевых показателей, подлежащих измерению. Более того, следует иметь в виду, что размер кластера, заявленный в описании плана выборки, будет, как правило, означать число домохозяйств, в то время как размер кластера для целей оценки эффекта схемы должен вместо этого означать обследуемую группу(ы) населения.

3.5.4. Расчет эффекта схемы (deff)

91. Указанные аналитиками фактические величины deff для переменных показателей обследования могут быть рассчитаны уже после завершения обследования. Это требует оценки вариантности выборки для выбранных переменных (соответствующие методы рассматриваются в главе 7), а затем расчета для каждой переменной величины соотношения ее вариантности к вариантности простой случайной выборки из такого же общего размера выборки. Этот расчет дает оценку «полного» показателя deff, включая эффекты стратификации, а также вариантность размеров кластеров, а не только лишь элемента, связанного с гнездовой группировкой.

92. Квадратный корень из соотношения величин вариантности дает коэффициент среднеквадратической ошибки или так называемый показатель deff, который часто рассчитывается на практике и заносится в техническую документацию таких видов обследований, как Обследования в области народонаселения и здравоохранения (OHЗ).

3.5.5. Число кластеров

93. Важно не упускать из виду, что размер кластера имеет большое значение и за пределами его воздействия на точность выборки и также играет важную роль применительно к общему размеру выборки, поскольку размер кластера определяет число различных адресов, которые необходимо посетить в ходе обследования. Такое существенное влияние на уровень затрат в ходе обследования – это, безусловно, именно та причина, по которой гнездовая выборка в первую очередь и применяется. Следовательно, выборка из 10 000 домашних хозяйств с кластерами размером в 10 домохозяйств каждый потребует 1000 кластеров, в то время как кластеры из 20 домохозяйствам потребуют только 500. Как подчеркивалось выше, чрезвычайно важно принимать во внимание факторы, как уровня затрат, так и точности при принятии решения по этой характеристике плана выборки. 

3.6. Поэтапная выборка

94. В теории идеальный план выборки при обследовании домашних хозяйств предполагает формирование выборки в произвольном порядке из n домашних хозяйств среди надлежащим образом определенных страт, составляющих генеральную совокупность домохозяйств, N. Полученная таким способом стратифицированная случайная выборка даст максимальный уровень точности. Однако использование выборки такого вида является слишком дорогостоящим делом для целей практической реализации¹⁰, как мы отметили выше при рассмотрении эффективности затрат, обеспечиваемой гнездовой выборкой.

3.6.1. Преимущества поэтапной выборки

95. Формирование выборки в несколько этапов имеет практические преимущества в плане самого процесса отбора. Это позволяет составителю выборки выделить с помощью последовательных шагов географические места проведения работ по обследованию, а именно по составлению списков и проведению опросов. Когда возникает необходимость в составлении списков по причине устаревшего инструментария выборки, для ограничения размеров района, по которому должны составляться списки, может вводиться этап отбора.

96. В случае гнездовой выборки, как правило, существуют не менее двух этапов процедуры отбора: первый этап – отбор кластеров и второй – отбор домашних хозяйств. В обследованиях домашних хозяйств кластеры всегда определяются как территориальные единицы того или иного вида. Если такие единицы достаточно малы с точки зрения как территории, так и численности населения, и если имеется их обновленный, полный и точный список, из которого можно сформировать выборку, тогда для плана выборки будет достаточно и двух этапов. Если наименьшая из имеющихся территориальная единица слишком велика для эффективного использования в качестве кластера, будут необходимы три этапа отбора.

Пример
Предположим, что та или иная страна хочет в качестве кластеров определить счетные участки переписи (СУ), поскольку это – наименьшая существующая административно- территориальная единица. Инструментарий СУ (более подробно вопрос инструментария рассматривается в главе 4) уже разработан, поскольку вся страна разбита на CУ. Он является точным, поскольку каждое домохозяйство по определению находится в одном единственном CУ. Более того, такой инструментарий вполне пригоден для применения в том смысле, что он базируется на последней переписи населения, при условии, что после этой переписи не было внесено никаких изменений в границы CУ. Предположим далее, что перепись проводилась два года назад. В связи с этим определяется необходимость в составлении более нового списка домашних хозяйств в СУ, вошедших в выборку, вместо того чтобы использовать полученный в результате переписи список домохозяйств двухлетней давности. Средний размер СУ составляет 200 домохозяйств, при том что желаемый размер кластера в целях проведения опросов определен в 15 домохозяйств на один кластер. Группа обследования проводит расчет, по которому стоимость составления списка из 200 домохозяйств ради тех 15, которые в конечном счете войдут в выборку (соотношение более 13 к 1), слишком велика. Затем составитель выборки принимает решение о проведении менее дорогостоящей операции на местах, в рамках которой каждый вошедший в выборку СУ будет поделен на квадранты приблизительно равного размера примерно по 50 домохозяйств в каждом. Затем план выборки модифицируется в сторону отбора одного квадранта или сегмента из каждого вошедшего в выборку СУ, в котором и будет проводиться составление списка, в результате чего объем работы по составлению списка снизится на три четверти. При таком плане действий мы имеем три этапа: первый этап – отбор СУ, второй этап – отбор сегментов СУ и третий этап – отбор домашних хозяйств.

3.6.2. Использование фиктивных этапов

97. Часто при формировании выборки используются так называемые фиктивные этапы, с тем чтобы уйти от необходимости на предпоследнем этапе делать выборку из огромного списка единиц. Этот список может содержать такое количество единиц и может быть столь громоздким, что он станет практически неуправляемым в ходе трудоемких операций ручного отбора. Даже если этот список сделан в виде компьютерного файла, он может быть все же слишком большим для эффективного управления им при формировании выборки¹¹. Фиктивные этапы позволяют сузить подсовокупности до более управляемых размеров, используя преимущества иерархической структуры административных единиц той или иной страны.

98. Например, для обследований сельского населения в Бангладеш деревни часто определяются в качестве единиц предпоследнего этапа формирования выборки. В Бангладеш существует более 100 000 деревень, и это, конечно, слишком много для управления процессом эффективного формирования выборки. Если план выборки предусматривает на предпоследнем этапе отбор, например, 600 деревень, то в случае Бангладеш в выборку будет включаться только одна деревня из 167. В целях сокращения размера файлов для формирования выборки может быть принято решение о формировании выборки в несколько этапов, используя иерархическую структуру единиц административно-территориального деления в Бангладеш, к которым относятся «таны» (thanas), «союзы» (unions) и деревни. Формирование выборки должно осуществляться поэтапно: сначала отбираются 600 танов при применении выборки с вероятностью, пропорциональной их размеру (этот метод подробно рассматривается в разделе 3.7). Затем из каждого вошедшего в выборку тана отбирается только один союз, снова при применении выборки с вероятностью, пропорциональной размеру, – таким образом в выборку войдут 600 союзов. На третьем этапе опять с применением выборки с вероятностью, пропорциональной размеру, одна деревня отбирается из каждого вошедшего в выборку союза, что в результате вновь даст 600 деревень. И наконец, выборка домохозяйств формируется из каждой отобранной деревни. Такая процедура в целом дает систематическую выборку всех домохозяйств по каждой отобранной деревне.

99. Описанная выше методология формирования выборки по сути является двухэтапной выборкой деревень и домохозяйств, хотя первоначально и были использованы два фиктивных этапа отбора танов и союзов, из которых затем были отобраны деревни. В этом случае необходимо математически пояснить фиктивный характер первых двух этапов путем изучения вероятностей на каждом этапе отбора, а также полной вероятности.

3.6.2.1. Первый этап отбора: таны

100. Таны отбираются на основе применения выборки с вероятностью, пропорциональной их размеру. На этом этапе вероятность определяется формулой:

где Р₁ – это вероятность отбора данного тана; a – число подлежащих отбору танов (в нашем примере – 600), а m_t – число сельских домохозяйств¹² в t-ом тане в соответствии с использованным инструментарием выборки (например, последняя перепись населения).

101. Знаменатель ∑mt – это общее число сельских домохозяйств во всех танах страны. Необходимо отметить, что фактическое число отобранных танов может быть менее 600. Это может произойти в том случае, когда один или более танов отбираются дважды, так как эта возможность существует для любого тана, показатель размера которого превышает интервал выборки. Интервал выборки при отборе танов определяется уравнением ∑mt ÷ a. Следовательно, если интервал выборки равен, скажем, 12500, а данный тан содержит 13800 домохозяйств, он будет автоматически отобран один раз и будет иметь вероятность 1300/12 500 быть отобранным дважды
(числитель дроби равен 13 800 – 12 500).

3.6.2.2. Второй этаn отбора: союзы

102. На втором этапе один союз отбирается из каждого вошедшего в выборку тана вновь на основе применения выборки с вероятностью, пропорциональной размеру. На практике это достигается путем составления списка всех союзов в отобранном тане, суммируя показатели их размеров, mu, и выбирая случайный номер между 1 и тt, т. е. показателем размера, вошедшего в выборку тана. Кумулянт, величиной которого является наименьший номер, равный или превышающий случайно выбранный номер, обозначает отобранный союз (либо для вы явления отобранного союза может использоваться равнозначная методика). Если тот или иной тан на первом этапе был отобран дважды, то из него отбирается то же самое число союзов. Вероятность на втором этапе определяется формулой:

где P₂ – это вероятность отбора данного союза из вошедшего в выборку тана; (1) означает, что отбирается только один союз, а m_u, – это число домохозяйств в u-ом союзе в соответствии с инструментарием.

3.6.2.3. Tpeтий этап отбора: деревни

103. На третьем этапе одна деревня отбирается на основе применения выборки с вероятностью, пропорциональной размеру, из каждого вошедшего в выборку союза. Вероятность на третьем этапе определяется формулой:

где P₃ – это вероятность отбора данной деревни из вошедшего в выборку союза; (1) означает, что отбирается только одна деревня, а t_v, – это число домохозяйств в v-oй деревне в соответствии с инструментарием.

3.6.2.4. Четвертый этап отбора: домашние хозяйства

104. На четвертом этапе мы исходим из допущения о том, что инструментарий в виде списка домохозяйств имеется по каждой вошедшей в выборку деревне, а значит, на базе данных списков может быть сформирована систематическая выборка домохозяйств. Из каждой вошедшей в выборку деревни отбирается фиксированное число домашних хозяйств, и это число является заранее определенным размером кластера. Вероятность на четвертом этапе определяется формулой

где P₄ – это вероятность отбора данного домохозяйства из вошедшей в выборку деревни, а b – это фиксированное число домохозяйств, отбираемых в каждой деревне.

3.6.2.5. Полная вероятность отбора

105. Полная вероятность является произведением всех величин вероятности на каждом этапе и определяется формулой:

Заменяя члены уравнения, получаем

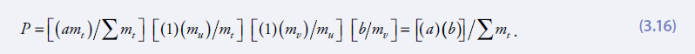
106. Следует отметить, что члены уравнения, P₂ и P₃, полностью взаимно исключается, показывая фиктивный характер «четырехэтапной» процедуры отбора. Следовательно, хотя таны и союзы физически и «отбираются», они тем не менее служат исключительно для выявления местоположения вошедших в выборку деревень. 

3.6.3. Двухэтапная схема

107. В последнее время много внимания уделяется использованию в развивающихся странах двухэтапной схемы планов выборки. Это – предпочтительный вариант плана выборки для Обследований по многим показателям с применением гнездовой выборки (ОМПГВ), проведенных Детским фондом Организации Объединенных Наций (ЮНИСЕФ) более чем в 100 странах, начиная с середины 1990-х годов. Кроме того, эти планы выборки преимущественно используются в Обследованиях в области народонаселения и здравоохранения (OH3).

108. Как правило, двухэтапная схема состоит просто из выборки, сформированной с вероятностью, пропорциональной размеру, и состоящей из нескольких сотен территориальных единиц, которые были надлежащим образом стратифицированы на первом этапе. Может быть составлен обновленный список домохозяйств как единиц выборки первого этапа, в зависимости от наличия информации, касающейся адреса и/или местоположения таких домохозяйств, и в зависимости от степени обновленности такой информации. Затем, на втором этапе следует систематическая выборка фиксированного числа домохозяйств. Территориальными единицами, обычно именуемыми «кластерами», как правило, являются деревни или счетные участки переписи в сельской местности и микрорайоны в городах.

109. Описанная выше двухэтапная схема привлекательна с многих точек зрения, но в основном в силу ее простоты. В целях снижения возможности ошибок регистрации данных при проведении выборочного обследования всегда предпочтительно при составлении плана выборки стремиться к упрощению, нежели к усложнению. Двухэтапная схема имеет целый ряд полезных характеристик, которые делают ее сравнительно простой и предпочтительной к использованию. Например:

• Как указывалось ранее, такой план выборки является самовзвешенным (все домохозяйства отбираются в выборку с равной вероятностью) или приблизительно самовзвешенным (вопрос различий между вероятностной выборкой, пропорциональной размеру, и вероятностной выборкой, пропорциональной предполагаемому размеру, рассматривается в разделах 3.7.1 и 3.7.2).
• Кластеры, определяемые в виде СУ или городских микрорайонов, в большинстве стран имеют удобный размер (не слишком большой), особенно в случае необходимости составления обновленного списка домохозяйств до окончательного этапа отбора.
• СУ, городские микрорайоны и большинство деревень обычно наносятся на карту либо для проведения работ переписи, либо в иных целях и имеют четкую делимитацию границ.

3.7. Выборка с вероятностью, пропорциональной размеру, и с вероятностью, пропорциональной предполагаемому размеру

110. В разделе 3.5 приведен пример, в котором при отборе кластеров для выборки применялась прежде всего выборка с вероятностью, пропорциональной размеру. В настоящем разделе метод выборки с вероятностью, пропорциональной размеру, рассматривается более подробно.

3.7.1. Выборка с вероятностью, пропорциональной размеру

111. Применение метода выборки с вероятностью, пропорциональной размеру, позволяет составителю выборки осуществлять более жесткий контроль над конечным размером выборки в обследованиях методом гнездовой выборки. В случаях, когда все кластеры имеют одинаковый или примерно одинаковый размер, не существует никаких преимуществ в применении выборки с вероятностью, пропорциональной размеру. Предположим, например, что каждый микрорайон данного города содержит точно 100 домохозяйств, и при этом требуется выборка из 1000 домохозяйств, распределенных по 50 вошедшим в выборку городским микрорайонам. Наиболее очевидным планом выборки будет формирование ПCB или, иными словами, равновероятностной выборки из 50 микрорайонов, а затем систематический выбор лишь одного из пяти домохозяйств из каждого микрорайона (также методом равновероятностной выборки).

Результатом будет выборка ровно 20 домохозяйств на каждый микрорайон, т. е. всего 1 000 домохозяйств. В этом случае уравнение отбора будет следующим:

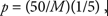
где р – это вероятность отбора домохозяйства;
(50/M) – вероятность отбора микрорайона;
М – общее число микрорайонов в городе, а (1/5) – вероятность отбора того или иного домохозяйства из определенного вошедшего в выборку микрорайона.

112. Значение сокращается до 10/M. Поскольку М является постоянной величиной, общая вероятность отбора для каждого вошедшего в выборку домохозяйства равна значению 10, деленному на число микрорайонов, М.

113. Тем не менее в реальных ситуациях микрорайоны или иные территориальные единицы, которые могут использоваться в качестве кластеров для обследований домашних хозяйств, редко имеют столь постоянные размеры. Применительно к приведенному выше примеру, они могут варьироваться по размеру в пределах, допустим, от 25 до 200. Равновероятностная выборка микрорайонов может привести к неудачной выборке из преимущественно малых или, напротив, больших микрорайонов. Результатом в этом случае может стать общий размер выборки, существенно отличающийся от заданных 1000 домохозяйств, которые приведены в этом примере. Одним из методов снижения возможности появления варьирующихся в широких пределах размеров выборки является создание страт, исходя из размера кластеров, и формирование выборки из каждой страты. Этот метод, как правило, не рекомендуется, поскольку он может снизить или усложнить использование других аспектов стратификации при формировании выборки. Предпочтительным решением в этом случае является применение выборки с вероятностью, пропорциональной размеру, поскольку она позволяет более жестко контролировать конечный размер выборки без необходимости введения стратификации по размеру.

114. Для иллюстрации применения выборки с вероятностью, пропорциональной размеру, мы начнем с выбора приведенного выше уравнения, однако выраженного в более формализованном виде для двухэтапной схемы¹³ следующим образом:

где P(αβ) – это вероятность отбора домохозяйства β в кластере α; P(α) – вероятность отбора кластера α; P(β|α – условная вероятность отбора домохозяйства β на втором этапе при условии, что кластер α был отобран на первом этапе.

115. Для фиксирования общего размера выборки с точки зрения числа домохозяйств нам необходима равновероятностная выборка n домохозяйств из совокупности в N домохозяйств. Следовательно, общая доля выборки составит n/N, что равняется P(αβ), как определено ниже. Далее, если число подлежащих включению в выборку кластеров обозначено как a, тогда в идеальном случае нам необходимо отобрать b домохозяйств из каждого кластера вне зависимости от размеров отобранных кластеров. Если мы определяем mi как размер i-ro кластера, тогда нам нужно, чтобы значение P(β|α) было равно b/тi. Следовательно,

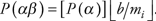
Поскольку n = ab, мы имеем ab/N=[Р(a)] [b/mi]

Решив последнее уравнение в отношении Р(a), мы получаем

116. Следует отметить, что N=⅀mi, и, таким образом, вероятность отбора кластера пропорциональна его размеру. Уравнение формирования выборки из единиц первого этапа с вероятностью, пропорциональной размеру, в которой конечные единицы тем не менее отбираются с равной вероятностью, будет иметь следующий вид:

117. Получаемый таким методом план выборки является самовзвешенным, что можно увидеть из уравнения (3.19), поскольку все члены уравнения являются постоянными величинами; напомним, что, хотя mi, является переменной величиной, сумма ⅀mi, – это константа, равная N. Приводимый ниже рисунок 3.2 может служить примером того, как сформировать выборку кластеров с вероятностью, пропорциональной размеру.

118. Что касается физического формирования выборки, следует отметить, что на рисунке 3.2 интервал выборки, I, последовательно добавляется к произвольно выбранной точке отсчета (RS) семь раз (или а-1 раз, где а – это число подлежащих отбору кластеров). Получаемые в результате числа отбираемых единиц составляют 311,2 (что является значением RЅ), 878,8; 1 446,4; 2 014,0; 2 581,6; 3 149,2; 3716,8 и 4 284,4. Кластером, включаемым в выборку в соответствии с этими восемью числами отбираемых единиц, в каждом случае является тот кластер, чей суммарный показатель размера представляет собой наименьшую величину, равную или превышающую число отбираемых единиц. Таким образом, кластер 03 выбран в силу того, что 377 – это наименьший кумулянт, равный или превышающий величину 311,2, а кластер 26 выбран в силу того, что 3744 – это наименьший кумулянт, равный или превышающий величину 3716,8.

119. Несмотря на то, что данная иллюстрация не очень убедительно демонстрирует эту закономерность (поскольку отобрано только восемь кластеров), выборка с вероятностью, пропорциональной размеру, имеет тенденцию отбирать скорее более крупные, нежели более мелкие кластеры. Это может быть очевидно, поскольку из формулы (3.17) следует, что вероятность отбора кластера пропорциональна его размеру; таким образом, кластер, содержащий 200 домохозяйств, имеет в два раза более высокую вероятность быть отобранным, нежели кластер из 100 домохозяйств. В связи с этим следует отметить, что один и тот же кластер может быть отобран более одного раза в случае, если его размер превышает интервал выборки, І. Однако ни один из кластеров на рисунке не соответствует этому условию, однако если это произойдет, то число домохозяйств, подлежащих отбору из такого кластера, должно удвоиться при двух «попаданиях», утроиться при трех попаданиях и т. д.

Рисунок 3.2. Пример систематической выборки кластеров с вероятностью, пропорциональной размеру

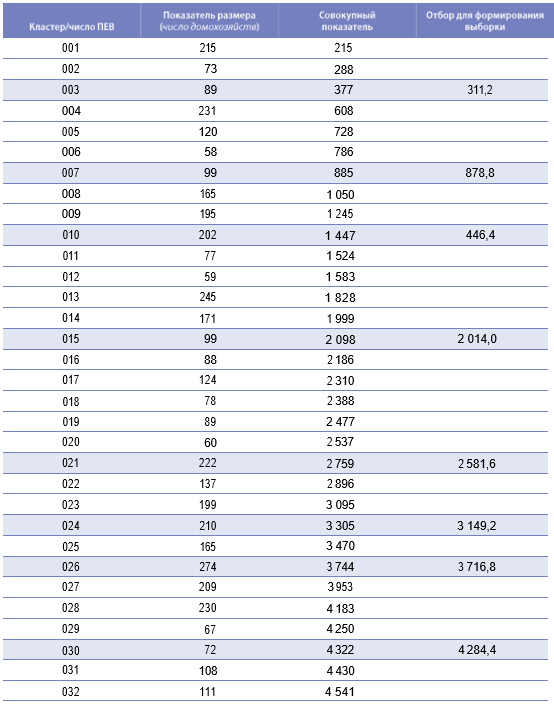
Инструкции по выборке: отберите 8 ПEB (кластеров) из 32 в данной совокупности, используя вероятность, пропорциональную размеру; в этом случае интервал выборки (I) будет равен 4541/8, или 567,6, где 4541 – это общий совокупный размер всех кластеров, а 8 – это число подлежащих отбору кластеров; произвольно выбранная точка отсчета (RS) – это случайное число между 0,1 и 567,6, выбранное по таблице случайных чисел; в данной иллюстрации RS = 311,2.

3.7.2. Выборка с вероятностью, пропорциональной предполагаемому размеру

120. Описанная в предыдущем разделе выборка с вероятностью, пропорциональной размеру, является в некоторой степени идеальным вариантом и в большинстве случаев не может быть осуществлена на практике. Это обусловлено тем, что показатель размера, используемый для установки уровня вероятности отбора кластера на первом этапе, зачастую не является фактическим показателем размера при формировании выборки домохозяйств на втором этапе.

121. В обследованиях домохозяйств в качестве показателя размера, обычно принимаемого на первом этапе отбора первичных единиц выборки или кластеров, выступает численность домохозяйств (или населения) из последней переписи населения. Даже если перепись проводилась совсем недавно, фактическая численность домохозяйств на момент переписи, скорее всего, будет отличаться, пусть и ненамного. Исключением, однако, является ситуация, когда отбор домохозяйств на втором этапе ведется напрямую из того же инструментария, который был использован для определения показателей размера (более подробно инструментарий выборки рассматривается в главе 4).

Пример
Предположим, что обследование домашних хозяйств проводится через три месяца после завершения переписи населения. Вместо составления нового списка домохозяйств в отобранных кластерах группа по проведению обследования принимает решение использовать на втором этапе двухэтапной выборки список переписи по домохозяйствам, поскольку достоверно считает, что такой список переписи является обновленным и точным для любых практических целей. На первом этапе формируется выборка деревень с использованием полученных в результате переписи данных о численности домохозяйств в качестве показателя размера для каждой деревни. Для каждой вошедшей в выборку деревни показатель размера, mi, идентичен фактическому числу домохозяйств, из которых должна формироваться выборка. Следовательно, если будет выбрана деревня А и если в ней по данным переписи находится 235 домохозяйств, то список, из которого будет формироваться выборка домохозяйств для обследования, также будет содержать 235 домохозяйств.

122. Однако многие обследования домашних хозяйств, базирующиеся на инструментариях переписи, проводятся спустя много месяцев, а иногда и лет после переписи (вопрос обновления инструментариев выборки подробно рассматривается в главе 4). В таких обстоятельствах зачастую принимается решение о проведении соответствующей работы на местах по подготовке нового списка домохозяйств в тех кластерах, которые отобраны для включения в выборку на ее первом этапе. Затем из такого обновленного списка формируется выборка домохозяйств для проведения обследования.

123. В приведенном выше примере данные переписи по численности домохозяйств выступают в качестве показателя размера, mi, который использовался для отбора кластера. Однако фактический список, из которого формируется выборка домохозяйств, будет иным. Он будет безусловно иметь другой показатель размера, который в определенной степени будет зависеть от величины промежутка времени между датами проведения переписи и подготовки списка обследования. Отличия возникнут в результате миграции населения в данный кластер и из него, строительства новых и сноса старых зданий, возникновения новых отдельных домохозяйств в случае брака (иногда в одной и той же жилищной единице с родителями) или случаев смерти. Когда выборка формируется с вероятностью, пропорциональной предполагаемому размеру, ее вероятность из уравнения отбора будет следующей:

где m_i` – это численность домохозяйств в соответствии с составленным списком, а другие члены уравнения определяются, как указывалось ранее.

124. Поскольку m_i`, и m_i, будут, скорее всего, отличаться в большинстве, если не во всех кластерах выборки, при расчете вероятности отбора (а, следовательно, и веса или, иными словами, обратной функции вероятности) необходимо учитывать эти отличия. Как показывает уравнение 3.20, каждый кластер будет иметь различный вес, не позволяя, таким образом, создать самовзвешенный план выборки.

125. Путем использования точных весовых коэффициентов для компенсации различий между показателями размера по данным переписи и обследования можно добиться неискаженных результирующих оценок обследования. Отсутствие надлежащей коррекции весовых коэффициентов дает смещенные оценки, причем величина погрешностей будет, без сомнения, возрастать по мере увеличения интервала времени между датами переписи населения и обследования. Необходимо отметить, однако, что при наличии между mi` и mi лишь небольших различий, выборка становится практически самовзвешенной, и при определенных обстоятельствах<sup>14</sup> целесообразно получать оценки обследования без взвешивания, поскольку погрешности будут весьма незначительными. Однако до принятия решения о данной схеме действий очень важно определить величины mi` и mi по каждому кластеру, чтобы эмпирически оценить, действительно ли различия минимальны.

126. Существует альтернативная стратегия, которую можно использовать для отбора домохозяйств на последнем этапе в тех случаях, когда применяется выборка с вероятностью, пропорциональной размеру, т.е. выборка, которая фактически является самовзвешенной. Эта стратегия предусматривает отбор домохозяйств с переменной долей выборки в рамках каждого кластера в зависимости от его фактического размера (эта стратегия рассматривается в следующем разделе).

3.8. Варианты формирования выборки

127. В данном разделе рассматриваются некоторые из многочисленных вариантов, которые можно применять при составлении надлежащей выборки для обследований общего назначения в отношении домашних хозяйств, при этом основное внимание уделяется стратегиям отбора на предпоследнем и последнем этапах, поскольку именно для этих этапов имеется несколько вариантов стратегий.

Кроме того, рассматривается вопрос выбора между равновероятностной выборкой или выборкой с вероятностью, пропорциональной размеру, для кластеров на предпоследнем этапе, а также между выборками домохозяйств с равномерной долей или с постоянным размером на последнем этапе. Далее в разделе дается резюме предыдущих разделов по таким вопросам, как контроль размера выборки, сравнение преимуществ и недостатков самовзвешенного и не самовзвешенного плана выборки, а также по другим вопросам типа рабочей нагрузки регистраторов. Кроме того, в разделе рассматриваются широко применяемые в настоящее время конкретные планы выборки, такие как использовались для Обследования в области народонаселения и здравоохранения и проведенного ЮНИСЕФ в середине десятилетия Обследования по многим показателям с применением гнездовой выборки. Эти схемы дают дополнительные варианты, достойные изучения, включая применение компактных (полных) и некомпактных кластеров.

3.8.1. Равновероятностная выборка, выборка с вероятностью, пропорциональной размеру, выборка с постоянным размером и с фиксированной долей

128. В таблице 3.4 возможные для применения схемы создают основу для обсуждения процедур, условий, преимуществ и недостатков различных планов выборки.

Таблица 3.4. Альтернативные планы выборки: два последних этапа отбора

129. Мы уже рассмотрели, что выборка с вероятностью, пропорциональной размеру, первичных единиц выборки или кластеров является более точным способом контроля конечного размера выборки, чем равновероятностная выборка, и это является ее главным преимуществом, особенно в том случае, если кластеры в широких пределах варьируются по числу входящих в каждый из них домохозяйств. Контроль над размером выборки важен не только в плане его влияния на расходы, но также и в плане того, что такой контроль позволяет руководителю обследования точно спланировать рабочую нагрузку регистраторов еще до начала проведения операций в рамках обследования. С другой стороны, равновероятностная выборка проще в осуществлении, нежели выборка с вероятностью, пропорциональной размеру, и ее применение имеет смысл в случаях, когда показатели размера кластеров примерно равны или отличаются незначительно. В практическом плане в случаях, когда фактической показатель размера отличается от указанного в инструментарии, вместо выборки с вероятностью, пропорциональной размеру, следует применять выборку с вероятностью, пропорциональной предполагаемому размеру.

130. Отбор фиксированного числа домохозяйств в каждом кластере выборки имеет два весьма важных преимущества: во-первых, точно контролируется размер выборки; во-вторых, этот метод предоставляет руководителю обследования возможность точно распределить рабочую нагрузку между регистраторами и, при их желании, выровнять эту нагрузку. При этом, однако, выборка с постоянным размером связана с определенными сложностями, поскольку она требует расчета различных интервалов выборки для каждого кластера. Применение различных интервалов выборки может вызвать путаницу и послужить источником ошибок. Тем не менее в этой схеме присутствует «встроенный» механизм контроля качества, поскольку число подлежащих отбору домохозяйств известно заранее. И все же указанные сложности могут привести к снижению эффективности из-за потерь времени на исправление ошибок отбора.

131. Формирование выборки с постоянным размером по определению требует составления списка домашних хозяйств, на основе которого отобранные домохозяйства могут обозначаться и выявляться. Наиболее часто в качестве такого списка выступает текущий список, подготовленный в рамках проводимых на местах подготовительных операций для обследования. Целесообразно организовать в центральном офисе проведение отбора подлежащих включению домохозяйств, причем это должно быть сделано другим сотрудником, а не самим составителем списка, для сведения к минимуму субъективности процедуры отбора.

132. В качестве альтернативы домашних хозяйств могут отбираться, исходя из фиксированной доли в каждом кластере. В этом случае отбор будет проще и менее подвержен ошибкам. Преимуществом при работе на местах является то, что такая выборка может осуществляться в процессе обхода регистратором кластера в целях составления обновленного списка домохозяйств. Это достигается путем разработки формуляра списка, включающего заранее подготовленные графы для выявления отобранных для выборки домохозяйств. Тот факт, что составление списка и формирование выборки могут осуществляться в ходе одного посещения, дает очевидную экономию затрат; однако такой подход имеет ряд существенных недостатков.

133. Одним из недостатков выборки с фиксированной долей является слабый контроль над размером выборки или рабочей нагрузкой регистраторов, за исключением случаев, когда показатели размера каждого кластера примерно равны. Другим, более серьезным недостатком является часто имеющий место субъективный выбор в результате того, что регистраторам доверяется фактический отбор домашних хозяйств для выборки или, иными словами, выявление тех домохозяйств, которые должны включаться в графы формуляров в списке выборки. Были проверены многочисленные исследования, которые продемонстрировали, что при контроле над ситуацией регистраторы имеют тенденцию отбирать более мелкие по размеру домохозяйства, и это подводит к выводу о том, что регистраторы для снижения своей рабочей нагрузки могут преднамеренно или неосознанно выбирать домохозяйства с меньшим числом респондентов.

134. Такой план является самовзвешенным и не зависит от конкретного набора процедур выборки на каждом этапе. Следовательно, двухэтапный план, объединяющий выборку кластеров с вероятностью, пропорциональной размеру, и выборку домохозяйств с постоянным размером, является самовзвешенным, в то время как комбинация выборки с вероятностью, пропорциональной размеру, и выборки с фиксированной долей самовзвешенной не является. Ниже рассматривается вопрос о том, какие из планов выборки в таблице 3.4 являются самовзвешенными.

3.8.1.1 План 1: Вероятность, пропорциональная размеру, постоянный размер кластера

Условия:

• различные показатели размера для совокупности кластеров;
• домохозяйства отбираются из тех же списков (например, список переписи домохозяйств), которые используются для определения показателей размера.

Преимущества:

• контроль над общим размером выборки и, следовательно, затратами;
• контроль над рабочей нагрузкой регистраторов;
• самовзвешенная выборка. 

Недостатки:

• выборка с вероятностью, пропорциональной размеру, несколько сложнее в применении, чем равновероятностная выборка;
• различные доли отбора для домохозяйств по каждому кластеру, что может стать источником ошибок.

3.8.1.1 План 1: Вероятность, пропорциональная размеру, постоянный размер кластера

135. Не существует приемлемых условий, при которых возможно использование такого плана выборки. Если кластеры различаются по размеру, тогда надлежащим планом выборки будет использование выборки с вероятностью, пропорциональной размеру, совместно с кластерами постоянного размера. Если кластеры имеют приблизительно равные размеры, тогда подходящей схемой является выборка с фиксированной долей, но при этом сами кластеры должны отбираться с помощью равновероятностной выборки.

3.8.1.3. План 3: Вероятность, пропорциональная предполагаемому размеру, постоянный размер кластера

Условия:

• различные показатели размера для совокупности кластеров;
• домохозяйства отбираются из новых списков, обновляющих списки инструментария для установления первоначального показателя размера.

Преимущества:

• контроль над общим размером выборки и, следовательно, затратами;
• контроль над рабочей нагрузкой регистраторов;
• является более точной, чем выборка с вероятностью, пропорциональной размеру, на основе данного инструментария, поскольку обновлены списки домохозяйств.

Недостатки:

• выборка с вероятностью, пропорциональной размеру, несколько сложнее в применении, чем метод равновероятностной выборки;
• различные доли отбора для домохозяйств по каждому кластеру, что может стать источником ошибок;
• не самовзвешенная выборка.

3.8.1.4. План 4: Равновероятностная выборка, с фиксированной долей

136. Не существует приемлемых условий, при которых возможно использование плана 4 по причинам, изложенным для плана 2.

3.8.1.5. План 5: Равновероятностная выборка, постоянный размер кластера

Условия

• показатели размера для совокупности кластеров примерно равны или варьируются в минимальных пределах.

Преимущества:

• контроль над общим размером выборки (но несколько слабее, чем в плане 1) и, следовательно, затратами;
• контроль над рабочей нагрузкой регистраторов, но также несколько слабее, чем в плане 1;
•  равновероятностную выборку легче применять, нежели выборку с вероятностью, пропорциональной размеру, или выборку с вероятностью, пропорциональной предполагаемому размеру.

Недостатки:

• различные доли отбора для домохозяйств по каждому кластеру, что может стать источником ошибок;
• не самовзвешенная выборка.

3.8.1.6. План 6: Равновероятностная выборка, с фиксированной долей

Условия

• показатели размера в совокупности кластеров практически равны. 

Преимущества:

• самовзвешенная выборка;
• предельная простота формирования выборки на обоих этапах.

Недостатки:

• слабый контроль над общим размером выборки с негативными последствиями для затрат и надежности данных, особенно в случае, если текущий показатель размера существенно отличается от показателя размера инструментария; а также негативные последствия для надежности данных, если выборка получается значительно меньше, чем планировалось;
• слабый контроль над рабочей нагрузкой регистраторов.

3.8.2. Обследование в области народонаселения и здравоохранения (OH3)

137. Несмотря на то, что в Обследовании в области народонаселения и здравоохранения (OH3) основной упор делается на женщинах детородного возраста, его план выборки подходит для обследований общего назначения.

138. В пособие по вопросам выборки Обследования в области народонаселения и здравоохранения, которое начиная с 1984 года широко используется во многих развивающихся странах, продвигается идея применения плана стандартных сегментов¹⁵ из-за его удобства и практичности. Стандартный сегмент определяется своим размером и составляет, как правило, 500 человек. Каждой территориальной единице страны, входящей в инструментарий выборки, присваивается показатель размера, рассчитываемый как численность населения этой единицы, деленная на 500 (или любой иной размер стандартного сегмента, принятый в данной стране). Результирующая величина, округленная до ближайшего целого числа, является числом стандартных сегментов в данной территориальной единице.

139. Выборка территориальных единиц с вероятностью, пропорциональной размеру, формируется с использованием стандартных сегментов в качестве показателя размера. Поскольку теми территориальными единицами, которые обычно используются на данном этапе выборки, выступают счетные участки (СУ), городские микрорайоны или деревни, показатель размера для большинства из них равняется единице или двум. В любой отобранной территориальной единице с показателем размера, превышающим единицу, проводится картографирование, в ходе которого создаются территориальные сегменты, при этом число таких сегментов равняется показателю размера. Таким образом, территориальная единица выборки с показателем размера 3 будет разделяться на карте на три сегмента примерно равного размера в тех пределах, в которых позволяют ее естественные границы, с точки зрения численности населения в каждом сегменте (в отличие от размера ее территории).

140. Каждая территориальная единица с показателем размера, равным 1, автоматически включается в выборку, а во всех остальных единицах произвольно отбирается один сегмент с помощью равновероятностной выборки. Затем проводится обход всех сегментов выборки, включая отобранные автоматически, для получения обновленных списков домохозяйств. Постоянная часть (доля) домохозяйств систематически отбирается из каждого вошедшего в выборку «кластера» для последующего проведения опроса в рамках OH3. Поскольку все сегменты имеют примерно равный размер, процедура выборки представляет собой двухэтапный план равновероятностной выборки сегментов и домохозяйств.

141. Используемый в OH3 план стандартных сегментов близок к указанному выше плану 6: равновероятностная выборка кластеров и выборка домохозяйств с фиксированной долей в рамках вошедших в выборку кластеров (также равновероятностную). Тем не менее благодаря процедуре разбивки на стандартные сегменты план OH3 не имеет тех серьезных недостатков, которые присущи плану 6: как общий размер выборки, так и рабочая нагрузка регистраторов, контролируется практически со 100-процентной точностью.

142. Важным преимуществом плана стандартных сегментов является значительное сокращение объема работ по составлению списков на предпоследнем этапе отбора. Для каждой территориальной единицы, состоящей из s сегментов, объем работ по составлению списков сокращается на 1/s (при наличии только одного сегмента объем работ не сокращается). Например, если данная территориальная единица содержит четыре сегмента, объем работ по составлению списков будет равен только одной четвертой части того объема работ, который потребуется для всей данной территориальной единицы. В связи с этой особенностью сократятся и затраты на подготовку выборки.

143. Даже при условии снижения затрат на составление списков, сокращение объема работ несет в себе определенные издержки. Недостатком плана стандартных сегментов является то, что для сегментов с показателем размера более 1 должно быть проведено картографирование. Такая работа по составлению карт может быть весьма трудоемкой и дорогостоящей, она требует особой подготовки и подвержена ошибкам. Тот факт, что естественные границы далеко не всегда четко показаны, препятствует обоснованной делимитации границ сегментов в рамках территориальной единицы. Этот недостаток усложняет работу регистраторов, которые позднее посещают такой сегмент, по установлению точного местоположения того или иного отобранного домохозяйства. Тем не менее эту проблему можно несколько упростить путем включения в список фамилии главы домохозяйства еще на этапе составления такого списка, и в этом случае плохо обозначенные границы приносят меньше неудобств.

3.8.3. Модифицированный план с применением гнездовой выборки: обследование по многим показателям с применением гнездовой выборки (ОМПГВ)

144. Специалисты-практики по проведению обследований зачастую жалуются на большие затраты и потери времени на составление списка домохозяйств в кластерах, включенных в выборку на предпоследнем этапе. Составление списков, как правило, требуется для большинства обследований – включая, как упоминалось выше, метод с использованием плана стандартных сегментов OH3 – для получения обновленного списка домохозяйств, из которого они должны отбираться для проведения опросов в рамках обследования. Это особенно важно в случаях, когда инструментарий выборки составлен более года назад. На работы по составлению списков приходится значительная доля расходов и процедур обследования, что зачастую упускается из виду на этапах кок планирования бюджета, так и составления графика обследования. Составление списков требует посещения районов обследования в дополнение к посещениям, необходимым для проведения опроса. Более того, число включаемых в список домохозяйств нередко в 5-10 раз превышает число домохозяйств, отобранных для опроса. Предположим, например, что план выборки предусматривает отбор 300 ПEB с размером кластера в 25 домохозяйств для проведения oпpoca в общей сложности 7500 домохозяйств. Если средняя ПEB предпоследнего уровня содержит 150 домохозяйств, тогда необходимо составить список из 45000 домохозяйств.

145. Стратегия выборки, использованная для Обследования с применением гнездовой выборки в рамках Расширенной программы вакцинации (PПB) (Всемирная организация здравоохранения, 1991 год), была разработана Центрами контроля заболеваний и частично Всемирной организацией здравоохранения (BO3) для того, чтобы избежать расходов и потерь времени, связанных с составлением списков. Обследование с применением гнездовой выборки PПB, предназначенное для оценки степени охвата детей вакцинацией, широко использовалось многими развивающимися странами в течение более двадцати лет. Важная статистическая проблема (Turner, Magnani and Shuaib, 1996) касается методологии формирования выборки. Методология обследований с помощью гнездовой выборки использует квотную выборку на втором этапе отбора, даже несмотря на то, что единицы первого этапа (деревни или микрорайоны) обычно отбираются в соответствии с принципами вероятностной выборки. Часто используемый, хотя и с вариациями, метод квотной выборки предусматривает начало проведения опросов в рамках обследования в некоторой центральной точке в отобранной деревне, а затем — продвижение в случайно выбранном направлении, продолжая опрос домохозяйств до выполнения установленной квоты. Согласно варианту обследования с применением гнездовой выборки PПB, посещение домохозяйств продолжается до тех пор, пока не будут найдены семеро детей из целевой возрастной группы. Хотя преднамеренное искажение и отсутствует при использовании таких методов, в течение длительного времени по ним высказывались различные критические замечания со стороны многих специалистов-статистиков, в том числе в работах Калтона (1987 год), Скотта (1993 год) и Беннетта (1993 год). Основной упор в критике делается на то, что эта методология не дает вероятностную выборку (см. раздел 3.2 по вопросу сравнения между вероятностной выборкой и другими методами выборки для обсуждения причин того, почему вероятностная выборка является рекомендуемым подходом для обследований домашних хозяйств).

146. Один из вариантов метода Обследования с применением гнездовой выборки PПB – так называемый план модифицированного обследования с применением гнездовой выборки (МОГВ) – был разработан в ответ на необходимость создания такой стратегии выборки, которая не предусматривала бы работ по составлению списков, но при этом базировалась бы на вероятностной выборке. Различные варианты плана МОГВ, а также другие планы были реализованы по всему миру в рамках проводимых под эгидой ЮНИСЕФ обследований по многим показателям с применением гнездовой выборки (ОМПГВ) для контроля выполнения определенных целей и задач Всемирной встречи на высшем уровне в интересах детей, касающихся положения детей и женщин (Международный фонд детского образования Организации Объединенных Наций, 2000 год).

147. План МОГВ является минималистской стратегией выборки. Он использует простую двухэтапную выборку, предусматривающую тщательную стратификацию, а также быстрый обход района и его разделение на сегменты. Работы по составлению списка не проводятся. План выборки с помощью МОГВ имеет следующие основные характеристики: 

• Формирование выборки территориальных единиц первого этапа, таких как деревни или городские микрорайоны, с применением выборки с вероятностью, пропорциональной размеру, или равновероятностной выборки в зависимости от уровня вариантности ПEB в отношении их показателей размера. Могут использоваться и старые показатели размера даже в том случае, если инструментарий выборки был сформирован уже несколько лет назад, но при этом такой инструментарий должен полностью охватывать обследуемую группу населения, как на национальном, так и на местном уровне.
• Посещение каждой территориальной единицы выборки с целью быстрого опроса населения, а также разбивка этой территории на сегменты с помощью существующих карт и картосхем, при этом число сегментов определяется заранее и равняется показателю размера согласно переписи, деленному на желаемый (ожидаемый) размер кластера. Создаваемые сегменты должны быть примерно равны по численности проживающего в них населения.
• Равновероятностный отбор одного территориального сегмента из каждой включенной в выборку ПEB.
• Проведение опросов всех домохозяйств в каждом отобранном сегменте.

148. Использование сегментации без составления списков является основным преимуществом плана согласно показателю размера. Он отличается от плана стандартных сегментов Обследования в области народонаселения и здравоохранения, который требует составления списка каждого сегмента. Работы по сегментации также частично вносят соответствующую поправку в случае использования инструментария, который может быть устаревшим. Хотя этот план имеет преимущество получения несмещенного результата, у него есть недостаток в плане более слабого контроля над конечным размером выборки, поскольку любой отобранный сегмент из-за роста населения может иметь гораздо более крупный размер, чем указано в инструментарии.

149. При этом, однако, составление карт требуется для плана согласно показателю размера точно так же, как и для плана стандартных сегментов Обследования в области народонаселения и здравоохранения со всеми присущими этой операции недостатками, которые отмечены в методе OH3. Кроме того, сложности могут возникнуть с созданием небольших сегментов, совпадающих по своему размеру с размером кластера, с четко обозначенными границами в случаях, когда таких естественных границ для малых территорий просто не существует. Есть и последний недостаток: в той степени, в которой тот или иной сегмент, где проводится опрос, является компактным кластером, т.е. все домохозяйства в нем территориально прилегают друг к другу, это дает более сильный эффект схемы в силу сравнительно высокой внутриклассовой корреляции, чем эффект, вызываемый некомпактными кластерами плана стандартных сегментов.

3.9. Специальные темы: двухэтапные виды выборки и формирование выборки для определения трендов

150. Данный раздел охватывает две специальные темы, связанные с составлением плана выборки для обследований домашних хозяйств: а) двухэтапная выборка, в рамках которой первый этап используется для краткого опроса в целях выявления среди членов домохозяйств лиц, относящихся к обследуемой группе населения, а второй этап предусматривает формирование выборки из тех лиц, которые отвечают определенным критериям; и b) методология формирования выборки, согласно которой обследование проводится повторно для оценки изменений или трендов. 

3.9.1. Двухэтапная выборка

151. Для обследований домашних хозяйств необходим особый вид плана выборки в том случае, когда не имеется достаточной информации для эффективного формирования выборки интересующей обследуемой совокупности. Такая необходимость, как правило, возникает, когда обследуемая совокупность представляет собой подгруппу населения – зачастую достаточно редкую, – члены которой присутствуют лишь в небольшой доле домохозяйств. Примерами могут служить лица определенной этнической группы, сироты или лица с доходом выше или ниже оговоренного уровня. Часто имеется возможность использовать тщательную стратификацию для выявления, например, территориальных единиц, где сконцентрированы интересующая этническая группа или лица с высоким доходом; однако, когда такие группы рассредоточены в относительно случайном порядке среди всего населения или когда какая-либо целевая группа – например, сироты – является редко встречающейся, тогда стратификация становится недостаточно эффективной стратегией, и должны применяться другие методы формирования выборки.

152. Одним из часто используемых методов является двухэтапная выборка, известная также как послестратификационная выборка или двойная выборка. Она осуществляется в четыре шага:

• а) формирование «крупной» выборки домохозяйств;
• b) проведение краткого проверочного опроса с целью выявления домохозяйств, члены которых относятся к обследуемой группе населения;
• с) последующая стратификация крупной выборки на две категории по результатам проверочного опроса;
• d) формирование подвыборки домохозяйств по каждой из двух страт для проведения второго, более подробного опроса целевой группы населения.

153. Целью такого двухступенчатого подхода является экономия затрат за счет проведения краткого проверочного опроса на этапе формирования первоначальной крупной выборки. За ним позднее следует более подробный опрос только в соответствующих критериям домашних хозяйств. По этой причине в качестве первоначальной выборки зачастую выступает выборка, сформированная для иных целей, а проверочный опрос делается в качестве «довеска» к опросу в рамках основного обследования. Таким образом, эта процедура позволяет выделить основные ресурсы на проведение второго этапа выборки и провести опрос на проверочном этапе в рамках весьма скромного бюджета.

Пример
Предположим, что планируется обследование 800 детей-сирот, проживающих в домохозяйствах родителей, здравствующих на момент опроса, или других родственников (в отличие от сирот, проживающих в специализированных учреждениях). Предположим далее, что согласно имеющимся оценкам для выявления 800 сирот необходимо включить в выборку 16 000 домохозяйств, т. е. 1 сирота на каждые 20 домохозяйств. Поскольку в связи со значительными расходами считается нецелесообразным формирование и опрос выборки из 16 000 домохозяйств ради проведения всего лишь 800 подробных опросов, принято решение использовать обследование общего назначения в области здравоохранения, которое также запланировано. Для обследования по вопросам здравоохранения сформирована выборка в 20 000 домохозяйств. Руководители обоих обследований договорились о том, что в вопросник обследования в области здравоохранения будет добавлен один дополнительный вопрос: «проживают ли в данном домохозяйстве лица в возрасте 17 лет или младше, у которых отец, мать или оба родителя умерли?» 

Такой дополнительный вопрос, как ожидается, позволит выявить домохозяйства, в которых проживают примерно 1000 сирот. Руководитель обследования по проблемам сирот затем сформирует подвыборку из 80 процентов таких домохозяйств для проведения подробного опроса.

154. Приведенный выше пример также показывает, в каких случаях двухступенчатая выборка является подходящей стратегией. Следует отметить, что обследуемый размер выборки в данном примере составляет лишь 800 сирот, но при этом размер выборки с точки зрения числа домохозяйств, необходимых для выявления нужного числа сирот, составляет 16 000. Следовательно, при расчете последнего числа (см. формулу 3.7) технический специалист по формированию выборки и руководитель обследования, скорее всего, придут к выводу о том, что двухэтапная выборка представляется наиболее практическим и эффективным с точки зрения затрат планом выборки.
155. Последующая стратификация выборки первого этапа важна по двум причинам. Проверочный вопрос или вопросы практически всегда должны быть краткими, поскольку они прилагаются к другому обследованию, который и без того вероятнее всего предусматривает продолжительный опрос. Руководитель основного обследования вряд ли согласится на развернутый набор проверочных вопросов. Следовательно, существует вероятность того, что в ряде домохозяйств из упомянутого выше примера, в которых были выявлены сироты, не будет детей-сирот – и наоборот. Такие ошибки неправильной классификации требуют формирования двух страт: одной – для домохозяйств с положительным результатом проверки, другой – с отрицательным результатом. Выборки для проведения полного опроса будут формироваться из каждой страты, исходя из возможности наличия неправильной классификации. Доля выборки для «положительной» страты должна быть очень высокой – до 100 процентов, в то время как для «отрицательной» страты подойдет гораздо более низкая доля выборки.

3.9.2. Выборка для оценки изменений или трендов

156. Во многих странах обследования домашних хозяйств планируются с двойной целью оценки а) базовых показателей (их уровней) при первоначальном проведении обследования и b) изменений этих показателей в ходе второго и последующих обследований. Когда обследование повторяется более одного раза, измеряются также тренды изменения показателей. Проведение повторных обследований оказывает различные виды воздействий на план выборки, которые не проявляются при проведении единовременного многопрофильного обследования. В частности, проблемами, вызывающими наибольшую озабоченность, являются: надежность оценки изменений и определение надлежащей комбинации в плане использования одних и тех же или разных домохозяйств от одного обследования к следующему. С последним аспектом связаны опасения по поводу субъективности ответов и нагрузки на респондентов, когда из раза в раз проводится опрос одних и тех же домохозяйств.

157. Рассмотрение проблемы надежности также требует математической иллюстрации. Мы начнем с рассмотрения вариантности оцениваемых изменений, d = р1 – р2, которые выражаются следующей формулой:

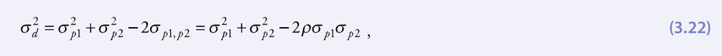
где величина р — это оцениваемая доля;

σ_d² — вариантность разности;
σ_p² — вариантность величины p при первом или втором раунде обследовании, которые обозначены цифрами 1 или 2;
σ_p1, p2 – ковариантность между р1 и р2;
и р – корреляция между полученными величинами p1 и p2 в ходе двух раундов обследования.

В тех случаях, когда оценка изменений незначительна, что случается достаточно часто, мы имеем тогда, σ_d² =2 σ_p² – 2р σ_p² (мы можем опустить нижние индексы 1 и 2). Следовательно,

158. Для оценки уравнения (3.22) следует отметить, что оценка σp2 для обследования с помощью гнездовой выборки является оценкой простой случайной выборки, ПCB, умноженной на величину эффекта схемы, deff. Корреляция р, которая имеет максимальную величину при использовании той же выборки домохозяйств, может достигать 0,8 или даже больше. В этом случае оценка s_d² величины σ_d² рассчитывается как:

159. При использовании одних и тех же кластеров, но других домохозяйств величина р все еще положительная, но значительно меньшая – вероятно в интервале от 0,25 до 0,35. Тогда мы имеем следующий результат (для р на уровне 0,3):

160. И, наконец, при полностью независимой выборке во втором раунде обследования при применении различных кластеров и различных домохозяйств р равняется нулю, и мы имеем:

При использовании типичного значения deff нa уровне 2,0 формула 3.19 дает следующий результат:

161. Для повторных обследований с использованием частичного наложения выборки, например 50 процентов одних и тех же кластеров/домохозяйств и 50 процентов – новых, величина р должна быть помножена на коэффициент F, равный доле совпадающей части выборки. В этом случае уравнение 3.16 приобретает следующий вид:

162. На основе указанных выше результатов можно сделать интересные выводы. Во-первых, оценка вариантности для сравнительно небольшого предполагаемого изменения между двумя обследованиями с использованием одной и той же выборки домохозяйств составляет всего около 40 процентов от уровня вариантности как по первому, так и по второму раунду обследования. Использование тех же кластеров, но других домохозяйств дает оценку вариантности на 40 процентов выше первого указанного уровня. Независимые выборки дают оценку вариантности в два раза выше этого уровня.

163. Следовательно, вариант с использованием одних и тех же домохозяйств при повторных обследованиях обладает существенными преимуществами с точки зрения надежности данных. При несоблюдении этого условия весьма значительное улучшение надежности достигается все же в случае использования либо a) доли одних и тех же домохозяйств, либо b) тех же кластеров, но с другими домохозяйствами. Обе стратегии дают результаты с более низкой вариантностью по сравнению с наименее удачным вариантом использования полностью независимых выборок.

164. Что касается проблемы ошибки регистрации данных, то наблюдается тем больше случаев возникновения двух негативных эффектов, связанных с респондентами – неполучение ответов и условный ответ, – чем чаще повторно используется одна и та же выборка домохозяйств. Респонденты не только все более неохотно принимают участие в опросах, увеличивая таким образом долю неполучения ответов в более поздних раундах обследования, но они также находятся под влиянием эффекта обусловливания, из-за чего при повторных опросах может снизиться качество их точности и ответов.

165. С указанным эффектом обусловливания связан феномен, известный как погрешность, вызванная «временем пребывания в выборке», когда ожидаются различные по величине оценки обследования от респондентов, ответы которых охватывают один и тот же период времени, но с разной степенью участия в данном обследовании. Этот феномен широко изучался, и было доказано его присутствие в обследованиях на самые различные темы: трудовые ресурсы, расходы, доходы и криминальная виктимизация. В Соединенных Штатах Америки, например, когда при проведении обследования рабочей силы респонденты опрашивались восемь раз, оценка уровня безработицы по ответам респондентов, в первый раз попавших в выборку, неизменно была примерно на семь процентов выше, чем в среднем по ответам респондентов за период проведения всех восьми опросов. Эта закономерность сохранилась в Соединенных Штатах в течение ряда лет. Анализируя эту погрешность, эксперты предположили, в том числе, что:

• регистраторы при последующих опросах могут не предоставлять респондентам такие же стимулы, как при первом опросе;
• респонденты могут узнать, что некоторые ответы вызывают дополнительные вопросы, и поэтому избегают давать определенные ответы;
• первый опрос может охватывать события, происшедшие за пределами учетного периода, в то время как в последующих опросах то или иное событие «привязано» к определенному сроку;
• респонденты действительно могут изменить свое поведение по причине участия в обследовании;
• респонденты могут быть не столь внимательны в плане предоставления точных ответов в последующих опросах, когда им наскучит сам процесс участия в обследовании (Kasprzyk, 1989). 

166. Следует отметить, что большинство из указанных выше причин применимо в основном к повторным опросам для одного и того же обследования; но, тем не менее, некоторые проявления такого же поведения респондентов могут иметь место и в случаях, когда одни и те же домохозяйства используются для различных обследований.

167. Из вышеизложенного можно сделать вывод, что существуют конкурирующие друг с другом эффекты при использовании:

• а) одной и той же выборки домохозяйств в каждом раунде обследования;
• b) замены домохозяйств для части выборки;
• с) новой выборки домохозяйств при каждом проведении обследования.

168. Если двигаться от а до с, то ошибка выборки по оценкам изменений увеличивается, в то время как ошибка регистрации данных имеет тенденцию к снижению. Ошибка выборки является наименьшей, когда в каждом случае используется одна и та же выборка домохозяйств в силу максимального коэффициента корреляции между измерениями. Противоположный эффект имеет место при использовании в каждом случае новой выборки домохозяйств.

169. Именно вариант b обычно рассматривается как наиболее компромиссный с точки зрения баланса ошибки выборки и погрешностей при регистрации данных. Если часть выборки сохраняется из года в год, ошибка выборки снижается по сравнению с вариантом с, а ошибка регистрации снижается по сравнению с вариантом а. Когда обследование проводится только в два раунда, наилучшим вариантом, по всей видимости, является вариант а. Воздействие респондентов, вероятно, не будет иметь слишком серьезных последствий для общего уровня ошибки обследования, когда выборка используется лишь дважды. Тем не менее наилучшим вариантом при повторном обследовании в три и более раундов будет вариант b. Удобной стратегией является замена в каждом раунде 50 процентов выборки по принципу ротации (примеры ротации выборки в эталонных выборках приведены в главе 4).

3.10. Если осуществление плана выборки нарушается

170. В настоящем разделе дается краткий обзор действий, которые необходимо предпринять в случае, если осуществление плана выборки сталкивается с какими-либо затруднениями, большинство из которых уже рассматривались или упоминались выше. При этом одним из важнейших принципов, который подчеркивается в этой и следующей главах, является то, что путем тщательного планирования во время составления плана выборки можно избежать многих препятствий в его осуществлении. Тем не менее, несмотря на самое тщательное планирование, могут возникнуть и непредвиденные проблемы.

3.10.1. Определение и охват обследуемого населения

171. Проблемы зачастую возникают по любой из множества причин, когда фактическая группа населения, охватываемая обследованием, не является его запланированной целевой совокупностью.
Пример

Рассмотрим обследование, в котором предполагается охватить типовую целевую совокупность в виде всего народонаселения страны.

Фактически численность охватываемого населения (т. е. то, из которого формируется выборка) зачастую меньше, чем общая численность населения по любой из следующих причин:

• в выборку не входят лица, проживающие в специализированных учреждениях, таких как больницы, тюрьмы и военные казармы;
• лица, проживающие в определенных географических районах, могут целенаправленно исключаться из охвата. К таким районам могут относиться труднодоступные местности; территории, пострадавшие от природных бедствий; объявленные закрытыми из-за гражданских волнений или войны; поселки или лагеря, где живут беженцы и иностранные рабочие, и т. д.;
• лица, не имеющие постоянного места жительства, рассматриваются как «не входящие в сферу охвата» обследования. К ним могут относиться кочевое население, команды судов, временные работники и т. д.

172. Проблемы, касающиеся таких подгрупп населения, применительно к плану выборки связаны с тем, что они обычно перед проведением обследования не определяются как группы, подлежащие исключению из сферы охвата обследования. В связи с этим осуществление плана выборки нарушается, когда случайно выбирается, скажем, а) какой-либо кластер, который вместо «традиционного» жилого района оказывается трудовым лагерем, тюрьмой или общежитием, или b) какая-либо ПEB расположена в горной местности и считается недоступной. Часто принимаемым в таких ситуациях «решением» является замена на другую ПEB. Такое решение, однако, означает появление погрешности в процедуре выборки.

173. Приемлемое решение заключается в том, чтобы избежать такой проблемы на этапе составления плана выборки. Это достигается, во-первых, за счет тщательного определения обследуемой группы населения и определения не только входящих в нее подгрупп, но и тех, которые должны исключаться из охвата. Во-вторых, инструментарий выборки должен быть затем модифицирован с целью удаления из него любых территориальных единиц, не входящих в сферу охвата обследования. Это относится и к исключению любых специально созданных счетных участков – например, трудового лагеря рабочих. В-третьих, выборка должна формироваться из такого модифицированного инструментария. Более подробно инструментарий выборки рассматривается в главе 4.

174. Следует также иметь в виду, что предложенное выше решение позволяет более точно определить целевую совокупность. Важно также дать описание точной целевой совокупности в отчетах обследования для надлежащего информирования пользователей.

3.10.2. Размер выборки слишком велик для бюджета обследования

175. Другая проблема возникает, когда расчетный размер выборки оказывается более крупным, чем может обеспечить бюджет обследования. Когда это происходит, группа по проведению обследования должна либо изыскать дополнительное финансирование обследования, или модифицировать цели обследования в части подлежащих измерению показателей, уменьшая либо требования по точности данных, либо число областей обследования.

176. Одним из путей уменьшения точности (повышения ошибки выборки) в целях значительного снижения затрат является отбор меньшего числа ПEB при сохранении, однако, общего размера выборки. Например, вместо 600 ПEB, состоящих из 15 домохозяйств каждая (n = 9 000), план выборки может быть изменен в сторону отбора 400 ПEB из 22 или 23 домохозяйств каждая (n = 9000). Что касается областей обследования, одно из решений может заключаться в том, чтобы ограничиться четырьмя основными регионами страны вместо, скажем, 10 провинций.

3.10.3. Размер кластера больше или меньше ожидаемого

177. Часто возникающая проблема состоит в том, что кластер выборки может значительно превышать свой показатель размера в результате, например, нового жилищного строительства, особенно в случае устаревшего инструментария выборки. Группа по проведению обследования может ожидать наличия 125 домохозяйств в заданном кластере, однако на этапе составления списка может обнаружить, что их количество составляет 400. Приемлемым решением в этом случае является разбивка кластера на территориальные подсегменты примерно равного размера с точки зрения их населения. Число сегментов должно равняться текущему количеству домохозяйств, деленному на первоначальный показатель размера, округленное до ближайшей целой величины. В нашем примере это будет значение 400/125 или 3,2, округленное до 3 сегментов. Эти сегменты должны создаваться путем нанесения их на карту и быстрого подсчета жилищных единиц (в отличие от домохозяйств). Затем для составления списка путем случайного выбора должен быть отобран один из сегментов.

178. Может также возникнуть и противоположная проблема. Кластер может оказаться значительно меньше ожидаемого в связи со сносом жилья, природным бедствием или по другим причинам. В этом случае часто возникает искушение заменить его на другой кластер, однако такой путь ведет к появлению погрешностей. Вместо этого меньший по размеру кластер должен быть использован таким, как он есть. Хотя это может привести к меньшему, чем целевой, конечному размеру выборки, возрастание ошибки выборки будет в конечном счете незначительным, если только не будет включено большое число таких кластеров. Использование меньшего по размеру кластера без изменения (или замены) позволит, тем не менее, получить несмещенную оценку, поскольку такой кластер является «репрезентативным» в плане текущих изменений его населения, происшедших с момента создания соответствующего инструментария.

3.10.4. Решение проблем, связанных со случаями неполучения ответов

179. Хотя эти случаи относятся скорее к проведению обследования, а не к осуществлению выборки, неполучение ответов представляет собой серьезную проблему, которая способна негативно повлиять на получение оценок обследования (проблема неполучения ответов подробно рассматривается в главах 6 и 8). Если допускается, что уровень неполучения ответов может превысить 10-15 процентов выборки, то возникающая в результате погрешность оценок может сделать их весьма сомнительными. И снова некоторые страны имеют тенденцию «решать» проблему неполучения ответов путем замены, не дающих ответа домохозяйств. Такой метод сам по себе ведет к погрешностям, поскольку взятые на замену домохозяйства все же представляют собой только ответившие домохозяйства, но среди них нет неответивших. Известно, что характеристики последних двух групп по важным переменным показателям обследования должны отличаться друг от друга, особенно в части социально-экономического положения. Предпочтительным решением, которое, к сожалению, никогда не дает 100-процентного успеха, является получение ответов от первоначально не ответивших домохозяйств. Это должно достигаться с помощью планирования с самого начала возможности нескольких повторных посещений не ответивших домохозяйств с целью добиться их сотрудничества (в случае отказа) или застать их дома (при отсутствии по тем или иными причинам). Может понадобиться до пяти повторных посещений, однако минимальным должно быть три посещения. 

3.11. Краткие рекомендации

180. В данном разделе дается краткое описание основных рекомендаций, которые необходимо вывести из этой главы. Хотя некоторые из рекомендаций применимы практически для любой ситуации (например, «использование вероятностной выборки»), есть другие рекомендации, для которых могут существовать исключения в зависимости от конкретных особенностей, ресурсов и требований той или иной страны. По этой причине руководящие указания, данные ниже в виде контрольного списка, представляется скорее в духе «эмпирических правил», а не как неизменные и непоколебимые рекомендации. Участники обследования должны стремиться:

• использовать методы вероятностной выборки на каждом этапе отбора;
• к максимальному упрощению, а не усложнению плана выборки;
• применять методы отбора, которые дают самовзвешенную или приблизительно самовзвешенную выборку в рамках областей обследования, а при отсутствии в плане таких областей – в рамках выборки в целом;
• использовать по возможности двухэтапный план выборки;
• рассчитывать размер выборки, используя формулу наподобие (3.5) и корректируя при необходимости величину постоянных параметров (таких, как прогнозируемая доля неполучения ответов и средний размер домохозяйства) с учетом специфики конкретной страны;
• использовать по умолчанию величину эффекта схемы на уровне 2,0 в формуле размера выборки, если для данной страны не имеется более точной информации;
• использовать в качестве основы размера выборки ту ключевую оценку, которая, как считается, будет охватывать наименьшую процентную долю совокупности среди всех ключевых оценок обследования;
• если позволяет бюджет, выбирать допустимый предел ошибки или уровень точности для ключевой оценки (см. выше) в размере 10 процентов от величины этой оценки, иными словами, относительная ошибка должна составлять 10 процентов при 95–процентной доверительной вероятности, или же добиваться уровня относительной ошибки в 12–15 процентов;
• выбирать первичные единицы выборки (ПEB) в качестве счетных участков переписи (СУ), если это удобно и возможно;
• использовать, где это возможно, неявную стратификацию совместно с систематической выборкой с вероятностью, пропорциональной размеру (BПP), особенно в многоцелевых планах выборки;
• ограничивать до абсолютно необходимого минимума число областей проведения оценки (для доведения размера выборки до управляемого уровня);
• добиваться достаточно большого числа (нескольких сотен) кластеров (или ПEB при двухэтапной выборке): чем больше, тем лучше;
• использовать небольшие размеры кластеров (10-15 домохозяйств): чем меньше, тем лучше; 
• использовать постоянный, а не переменный размер кластера, иными словами, фиксированное число домохозяйств вместо постоянной доли выборки;
• применительно к областям обследования добиваться минимально количества, равного 50 ПЕВ в каждой области;
• планировать минимум три, а предпочтительно – пять повторных посещений для решения проблемы неответивших домохозяйств;
• для редких подгрупп населения изучать возможность использования двухэтапной выборки путем включения «дополнительного» вопроса в уже запланированное крупное обследование в целях выявления обследуемых лиц и последующего подробного опроса в рамках под выборки;
• применительно к обследованиям, предназначенным для измерения происшедших изменений, проводить опрос одних и тех же домохозяйств в обоих раундах только в том случае, если запланировано всего два опроса; при тpex и более опросах использовать схему частичного совпадения выборки путем ротации новых домохозяйств в рамках выборки в каждом раунде. 

1. ^ В настоящее время стандартной практикой многих проводящих обследования организаций является обеспечение того, чтобы определение домохозяйств для включения в выборку проводилось в кабинетных условиях, где этот процесс легко поддается надзору со стороны контролеров. Более того, выборка должна формироваться сотрудником, который не участвовал в создании списка домашних хозяйств до начала формирования выборки или не знаком с фактическим положением дел на местах.
2. ^ Несколько парадоксальным является тот факт, что формула расчета размера выборки требует знания приблизительной величины оценки, подлежащей измерению. Эту величину, однако, можно «предположить», используя различные методы, например, путем использования данных переписи или аналогичного обследования, данных по соседней стране, экспериментального обследования и т. д.
3. ^ Это справедливо для любых случаев, когда требуется одинаковый уровень надежности для каждой из областей обследования.
4. ^ Такое решение может быть принято, например, если предполагаемые относительные среднеквадратические ошибки для (любого из) ключевых городских показателей будут выше, к примеру, на 7,5 процента (95-процентная доверительная вероятность составит 15 процентов, что в настоящем руководстве рассматривается как максимально допустимый уровень).
5. ^ Формула для размера выборки может также содержать некий множитель, так называемый поправочный множитель на конечности выборки, который необходимо учитывать в случаях, когда результирующий расчетный размер выборки составляет значительную долю размера совокупности. Однако это условие редко возникает применительно к крупномасштабным обследованиям домашних хозяйств тех типов, которые рассматриваются в данном руководстве. В нашем случае поправочный множитель на конечности выборки принимается за 1,0 и, следовательно, не учитывается в формуле 3.5. 
6. ^ Поскольку величина r в данном случае применяется ко всей совокупности, она равняется р, поэтому е
   равняется 0,10p. 
7. ^ Оптимальное распределение означает распределение на основе стоимостных функций и различных величин вариантности в рамках страт (мер неоднородности). Этот метод не рассматривается в данном руководстве, поскольку он редко используется на практике в развивающихся странах. Это может быть обусловлено отсутствием точных цифр по расходам на операции обследования. Читатель может найти подробную информацию по оптимальному распределению во многих ссылках, указанных в конце данной главы. 
8. ^ Неудачная стратификация имеет место при создании страт без необходимости, или когда некоторые элементы совокупности неправильно классифицированы и отнесены к неверной страте. 
9. ^ Важно отметить, что стратификация и гнездовая выборка не являются конкурирующими друг с другом вариантами плана выборки, поскольку оба этих метода неизменно используются в выборке обследований домашних хозяйств.
10. ^ Существует всего лишь несколько исключений, и они касаются стран с очень небольшой территорией, таких как Кувейт, где формирование случайной выборки домохозяйств будет связано с очень низкими транспортными расходами.
11. ^ Тем не менее существует возможность сделать весьма большой компьютерный файл более приемлемым для формирования выборки, например, путем разбивки его на отдельные подфайлы для каждой страты или административной единицы (например, региона или провинции).
12. ^ Это – единица размера, и она может в качестве варианта отображать численность населения тана при том условии, что используемое число совместимо со всеми единицами размера на каждом этапе.
13. ^ См. (Kalton, 1983, pp. 38-47), где подробно изучается данное понятие и рассматривается метод выборки с вероятностью, пропорциональной размеру. 
14. ^ Такая стратегия применима в тех обследованиях, в которых оценки ограничены долями, соотношениями и коэффициентами; однако в тех обследованиях, в которых необходима оценка суммарных или абсолютных величин, необходимо использование весовых коэффициентов вне зависимости от того, является ли или нет выборка самовзвешенной, приближенно самовзвешенной или не самовзвешенной. 
15. ^ План стандартных сегментов также использовался в программе обследований 1980-1990-x годов Панарабского проекта по проблемам развития детей (ПАПЧАЙЛД) — см. Лига арабских государств (1990 год).